黄酒发酵的实质是一个多变量输入、输出的生物化学反应过程,麦曲、酵母、大米在不同环境条件下相互作用,生成了糖类、有机酸、乙醇、酯类、醛类、氨基酸等各种代谢产物[1-2]。黄酒发酵工艺主要分为传统手工酿造、机械化酿造2种[3]。一方面,手工酿造依赖酿酒师的人工经验,已逐渐不能适应工业化生产和控制的需求;另一方面,机械化新工艺的黄酒发酵过程难以实时监测和控制,黄酒品质稳定性差,其自动化水平落后于其他工业生产。2021年,《“十四五”智能制造发展规划》中提出,加快轻工、食品行业的智能和绿色制造升级,如何实现黄酒发酵自动化控制是黄酒产业面临的关键问题。
目前关于黄酒发酵自动化的研究主要分为2个方面。一是对发酵过程中的环境变量进行监测和控制。徐玲等[4]针对黄酒发酵过程中温度控制存在的延迟问题,设计了数字式Smith预估增量比例-积分-微分(proportion integration differentiation,PID)控制器,但发酵过程中关键生物变量却鲜有涉及;二是对黄酒发酵过程建立数学模型。LIU等[5-7]探讨了4种酶、酒曲和3个发酵温度对黄酒发酵过程中糖类、有机酸、甘油、乙醇的影响,为黄酒发酵的建模提供了理论基础;针对发酵过程中主要生化反应和初级产物,提出了不同温度条件下同时糖化发酵的动力学模型(simultaneous saccharification and fermentation,SSF);还针对工业生产中黄酒前酵阶段,建立了工业生产中同时糖化发酵模型SSF,并采用Marquardt方法对模型参数进行了辨识;宗原等[8]针对基于Levenberg-Marquardt易陷入局部最优解,收敛速度慢的问题,提出了具有莱维飞行机制和柯西变异的蚁狮优化算法,提升了固定温度条件下SSF模型的精度。一方面上述模型只适用于特定的温度条件,模型的通用性不高;另一方面,黄酒发酵过程是非线性,基于发酵动力学的SSF模型的拟合效果较差。
针对上述黄酒发酵数学模型中的问题,本文分别从建模方法和优化方法2个维度进行了研究:a)在系统建模方法中,模糊系统由于其良好的可解释性及强大的学习能力得到了广泛的关注[9-11],其中自适应神经模糊推理系统(adaptive network-based fuzzy inference system,ANFIS)[9]将模糊逻辑与神经网络结合,可以很好地处理非线性问题;b)在优化方法中,通过模拟自然界中生物行为或物理现象的元启发式算法常被用来解决各种学科领域的最优化问题[12-19],常见的有粒子群算法(particle swarm optimization,PSO)[15]、随机分形搜索算法(stochastic fractal search,SFS)[16]等。
本文针对黄酒发酵产物多样性的特点,首先提出了多输出自适应神经模糊推理系统(multi-output adaptive network-based fuzzy inference system,MOANFIS);其次将层次学习粒子群算法(level-based learning swarm optimizer,LLSO)[20]中的层次学习策略与莱维飞行结合,提出了层次学习的随机分形搜索算法(level-based learning stochastic fractal search,LLSFS),该算法在面对高维优化问题时,具有优秀的全局搜索能力;最后,将LLSFS算法用于MOANFIS模型的优化,并与其他算法进行比较。
1 多输出自适应神经模糊推理系统
ANFIS是基于T-S模糊系统[21]而建立的,既可以利用神经网络的学习机制自动从输入输出数据中提取规则,又兼具有模糊系统清晰的语言表达能力,但是其只有一个输出结点。黄酒发酵过程是一个多变量输入、输出的系统,本文将ANFIS的单维输出拓展为多维输出,即MOANFIS,其结构如图1所示,其中长方形结点表示含有系统参数的自适应结点,圆形结点表示无系统参数的固定结点。

图1 MOANFIS结构图
Fig.1 Structure of MOANFIS
对于k维输出的模型,假设训练数据集为D=(X,Y),其中X=(x1,x2,…,xN)∈Rn×N是输入数据,Y=(y1,y2,…,yk)∈Rk×N是真实的输出数据,训练集大小为N。 xi=![]() 是第i个(i=1,…,N)实例的n维特征向量,
是第i个(i=1,…,N)实例的n维特征向量,![]() 是第i个(i=1,…,n)实例的k维标签向量。第j层结点的输出记为Oj(j=1,2,…,5)。
是第i个(i=1,…,n)实例的k维标签向量。第j层结点的输出记为Oj(j=1,2,…,5)。
第1层:模糊层。对输入数据进行模糊化操作,计算每个维度特征的隶属度。本文选取高斯函数作为隶属度函数,Ai,j(i=1,…,n;j=1,2)是每个特征对应的模糊集。该层输出如公式(1)所示:

(1)
式中:cij,σij分别为高斯函数的均值和标准差,是模糊规则的前件参数。
第2层:规则的权重层。该层实现了模糊推理过程,每个节点的输出表示某一条规则的可信度,如公式(2)所示:
(2)
第3层:规则的权重归一化层,如公式(3)所示:
(3)
第4层:模糊规则输出层。对于一个n维的输入向量x=(x1,x2,…,xn),k维输出向量的MOANFIS,其第l个规则表示如公式(4)所示:
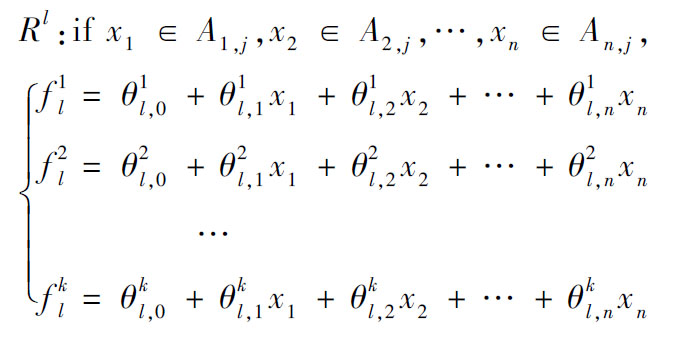
(4)
式中:A1,j,A2,j,…,An,j(j=1,2)表示模糊子集,θ[l]∈R(n+1)×k表示是对应于k维输出向量的第l个模糊规则的后件参数矩阵,所有模糊规则的后件参数矩阵为θ=(θ[1],θ[2],…,θ[r])∈Rr×(n+1)×k。每个模糊规则都共享模型的前件参数,本层输出如公式(5)所示:
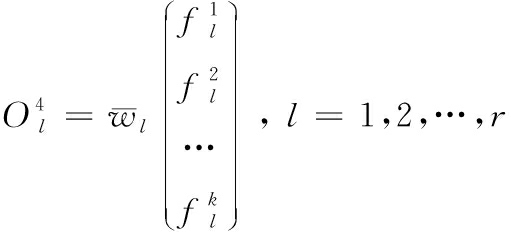
(5)
第5层:输出层,如公式(6)所示:
![]() t=1,2,…,k
t=1,2,…,k
(6)
通过后件参数矩阵θ的拓展,MOANFIS具备了多维输出的能力,其输出为![]()
对于大小为N的训练数据集D来说,其真实输出为Y=(y1,y2,…,yN)T,MOANFIS模型的预测输出为![]() 对MOANFIS模型预测性能的评估可采用均方误差(mean square error,MSE)来衡量,如公式(7)所示:
对MOANFIS模型预测性能的评估可采用均方误差(mean square error,MSE)来衡量,如公式(7)所示:
(7)
2 多输出自适应神经模糊推理系统的优化
2.1 随机分形搜索算法
SFS[16]是Salimi模仿自然界中的物理扩散现象提出的一种智能优化算法。简单起见,初始粒子位于平面原点,然后往周围随机扩散生成其他粒子。重复这个过程,直到形成一个分支状结构的簇。粒子分形过程如图2所示。

图2 粒子分形示意图
Fig.2 Demonstration of particle diffusion
FS算法主要有2个阶段:分形阶段和更新阶段。前一个过程中,每个粒子在其当前位置周围扩散,增加了找到优化函数全局最小值的机会,也避免了陷入局部最小值。后一种过程中,算法模拟了一个粒子根据其他粒子的位置更新自己的位置。为了避免粒子扩散导致粒子数量急剧增加,SFS考虑的是一个静态扩散过程,即扩散过程中产生的最佳粒子是唯一被考虑的粒子,其余的粒子被丢弃,同时算法还使用了一些随机方法参与更新的过程。详细内容请参考原论文。
2.2 对随机分形搜索算法的改进
SFS算法中第二阶段的更新过程中,是基于最佳粒子或随机挑选粒子对整个种群进行的更新。随着优化问题维度的增加,局部最优解增多,粒子易陷入局部最优点而导致算法过早收敛。针对此问题,本文将LLSO[20]中的层次学习策略与莱维飞行结合后,改进了SFS中第二阶段的对粒子的更新方式,提出了LLSFS算法。
2.2.1 层次学习策略
LLSO根据粒子对应的函数适应度值将其划分成为不同的等级,好的粒子具有更高的等级,对应于更小的层级号。层次学习策略如图3所示。

图3 层次学习的结构图
Fig.3 Framework of Level-Based Learning
首先,粒子群中各粒子根据其对应的函数适应度值升序排列,并划分成4个等级L1~L4。L4中的粒子向L1~L3中的粒子学习,L3中的粒子向L1~L2中的粒子学习,L2中的粒子向L1中的粒子学习,L1中的粒子不进行更新直接进入下一次循环中。粒子的更新方式如公式(8)所示:
![]()
(8)
式中:Pi,j位于第Li层的第j个粒子,Vi,j是其速度。Prl1,k1和Prl2,k2分别是从更高的2个层中rl1和rl2中随机挑选出的2个粒子,k1和k2表示各自层中的粒子的索引值。Lrl1层级高于Lrl2层级,即Prl1,k1粒子优于Prl2,k2粒子。r1、r2和r3是[0,1]之间的随机数,φ是[0,1]之间的随机数。
层次学习策略具有以下特点:一方面,更高等级的粒子指引种群朝着全局最优解的方向进化,进而获得较快的收敛速度;另一方面,处于低层级的粒子有着更强的空间探索性能表现。
2.2.2 莱维飞行的层次学习策略
为了更好地提升算法的全局搜索能力,避免早熟收敛,本文将莱维飞行融入层次学习策略中。莱维飞行是服从莱维分布的随机搜索方法,在面对大范围空间的优化问题上有着良好的表现[22]。其函数表达如公式(9)所示:
(9)
式中:ra和rb是[0,1]之间的随机数,β是值为1.5的常量,σ计算如公式(10)所示:

(10)
式中:Γ(x)=(x-1)。
L3和L4中的粒子有着更好的空间搜索能力,利用莱维飞行对其中粒子优化,粒子更新方式如公式(11)所示:

(11)
2.2.3 层次学习随机分形搜索算法
LLSFS算法步骤如下:
步骤1:初始化粒子群P,计算每个粒子对应的函数适应度值F;
步骤2:进入迭代循环;
步骤3:粒子分形生成新粒子群Ptemp,计算粒子对应的函数适应度值Ftemp;
步骤4:根据Ftemp大小,对粒子群Ptemp进行排序,适应度值小的粒子保留;
步骤5:粒子群Ptemp分为4个层级,使用莱维飞行的层次学习策略生成新的粒子群Pnew,计算对应的函数适应度值Fnew;
步骤6:如果Fnew<Ftemp,迭代继续。
3 结果与分析
3.1 黄酒发酵数据集
本文数据来自女儿红酒厂黄酒前酵过程采集到的数据,5个生产批次共计212组数据样本。4个发酵罐中170组数据作为训练集,一个发酵罐中42组数据作为测试集。各维度数据之间差异大,故对数据进行了归一化,取值范围为[0,1]。输入数据分别为:发酵过程的采样时间(h)、温度(T)、pH值、总糖质量浓度、总酸质量浓度、酒精度;输出数据分别为:下一时刻的总糖质量浓度(h+2)、总酸质量浓度(h+2)、酒精度(h+2)。
3.2 实验设置
本文采用的实验平台为:Window 10操作系统,主频为2.9 GHz的Intel i5处理器,内存为8 GB,编程环境为MATLAB2020b。
对于MOANFIS,人工设定的参数采用如下方式:a)采用网格方式获得模型的前件参数,即每个输入隶属度函数组合,对应一个模糊规则;b)采用加权适应度函数,即![]() 对模型进行迭代训练。发酵产物中有机酸含量偏小,为了提升模型对有机酸的预测能力,本文加大了其在适应度函数公式中的权重,k1和k3的值分别设置为1,k2的值设置为5。
对模型进行迭代训练。发酵产物中有机酸含量偏小,为了提升模型对有机酸的预测能力,本文加大了其在适应度函数公式中的权重,k1和k3的值分别设置为1,k2的值设置为5。
本文分别采用PSO、SHADE[14]、WOA[17]、SSA、AVOA[19]、SFS与LLSFS进行实验对比,对MOANFIS模型的参数进行寻优。LLSFS算法种群规模设置为48以保证层次学习中每层粒子数量相同,其余算法的种群规模为50。迭代次数为200次。
3.3 实验结果及分析
本文分别使用上述各算法对MOANFIS模型的适应度函数F独立实验10次。从实验结果的最优值、平均值和方差3个维度评估各算法的性能。实验结果表明,LLSFS算法在3个评价指标上均有着更好的表现。相比于SFS算法,LLSFS算法有着更快的收敛速度,全局搜索能力、鲁棒性也得到进一步的提升。各算法的实验结果如表1所示,图4展示了各算法的收敛曲线。
表1 训练集适应度值F
Table 1 Fitness value F on training dataset

算法最优值平均值方差PSO0.096 70.120 44.936 4e-04SHADE0.098 80.118 02.869 8e-04WOA1.491 31.927 80.207 1SSA0.700 51.295 00.262 7AVOA0.086 50.103 62.386 7e-04SFS0.046 60.047 91.572 4e-06LLSFS0.044 50.045 81.406 4e-06

图4 各算法对MOANFIS的收敛曲线
Fig.4 Convergence curve of each algorithm to MOANFIS
模型的优劣主要取决了其在测试集上表现。本文分别从MSE、平均绝对值误差(mean absolute error,MAE)、决定系数R2 3个评价指标考察MOANFIS模型的精度和泛化能力。首先将模型预测数据进行反归一化还原为真实尺度的发酵数据,然后分别使用各评价指标进行分析。MSE的计算使用公式(7),MAE和R2的计算方式如公式(12)和公式(13)所示:
(12)
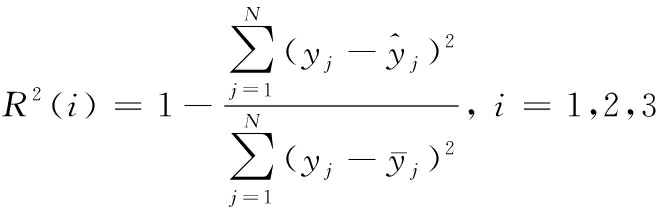
(13)
实验结果表明,相比于其他算法,LLSFS-MOANFIS模型对下一时刻的总糖质量浓度、总酸质量浓度、酒精度均有着更准确地预测结果。从指标R2来看,LLSFS-MOANFIS模型的总糖质量浓度和酒精度的R2值分别为0.96和0.963,预测效果良好,但总酸浓度R2值为0.615,预测效果还有进一步提升的空间。实验结果如表2所示。
表2 测试集实验结果
Table 2 Experimental results on testing dataset

算法下一时刻总糖质量浓度下一时刻总酸质量浓度下一时刻酒精度MSEMAER2MSEMAER2MSEMAER2PSO166.11110.9600.4220.0640.1830.5536.3021.7630.603SHADE92.1728.4370.6800.0690.2120.5176.8861.6950.567WOA299 5.09041.660-9.4181.1880.985-7.276206.40511.688-11.989SSA733.84323.501-1.5520.2560.400-0.78240.0705.246-1.521AVOA76.0966.2900.7350.0850.2340.4069.1512.7430.424SFS37.8805.7640.8680.0870.2280.3942.4181.2620.848LLSFS11.4502.4500.9600.0560.1790.6150.5880.5930.963
本文将LLSFS-MOANFIS模型与基于发酵动力学的SSF[7]模型进行了对比。SSF模型分别针对3批黄酒发酵数据建立了不同模型,并未探讨模型的泛化能力,但也有较好的参考价值。本文的测试集是和其论文中12罐的发酵数据是同一批数据,选用该批次数据进行实验结果的对比分析。除了LLSFS-MOANFIS模型的总酸质量浓度R2表现不佳之外,其余各项指标中LLSFS-MOANFIS模型的拟合效果均优于SSF模型。结果如表3所示。
表3 SSF和LLSFS-MOANFIS的对比
Table 3 Comparison of SSF and LLSFS-MOANFIS
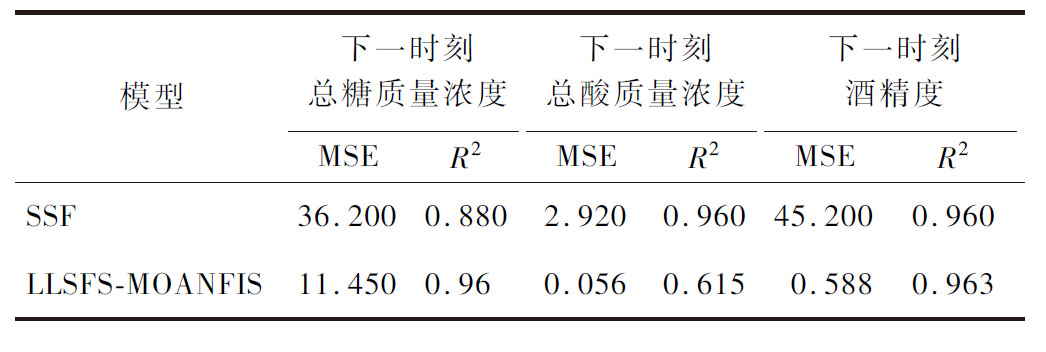
模型下一时刻总糖质量浓度下一时刻总酸质量浓度下一时刻酒精度MSER2MSER2MSER2SSF36.2000.8802.9200.96045.2000.960LLSFS-MOAN-FIS11.4500.960.0560.6150.5880.963
图5展示了LLSFS-MOANFIS模型在测试集上预测效果。从图中可以看出,LLSFS-MOSNFIS对下一时刻总糖质量浓度、酒精度的拟合效果良好,但是对下一时刻总酸质量浓度的预测表现还有可提升的空间。一方面由于黄酒发酵过程中产生的有机酸是微量物质,不同批次之间的总酸质量浓度差异较大;另一方面,总酸质量浓度的数据分布较为分散,离群点较多,影响了拟合效果。

a-下一时刻总糖浓度预测;b-下一时刻总酸浓度;c-下一时刻酒精度预测
图5 LLSFS-MOANFIS在测试集上的实验结果
Fig.5 Experimental results of LLSFSOMOANFIS on testing dataset
4 结论
本文针对黄酒发酵醪液中监控目标产物多样的特点,提出了一种具有多输出结构的MOANFIS模型,建立了当前时刻的发酵数据为输入,下一时刻关键发酵数据为输出的模型结构。同时本文提出的LLSFS算法对MOANFIS模型的参数进行了辨识优化,实验结果表明LLSFS算法有着更好的全局搜索能力和鲁棒性,提升了MOANFIS的精度。基于模糊系统理论的黄酒发酵建模研究工作为黄酒建模开辟了新的方向。
[1] 吴宗文, 孙军勇, 吴殿辉,等.绍兴黄酒发酵过程中有机酸及产酸细菌的初步研究[J].食品与发酵工业, 2016, 42(5):12-18.
WU Z W, SUN J Y, WU D H, et al.Preliminary study on organic acid and acid-producing bacterial during Chinese rice wine fermentation[J].Food and Fermentation Industries, 2016, 42(5):12-18.
[2] 胡武瑶, 杨昳津, 窦慧, 等.不同麦曲酿造黄酒中挥发性风味物质的代谢差异[J].食品与发酵工业, 2020, 46(8):226-233.
HU W Y,YANG Y J,DOU H,et al.Metabolic differences of volatile flavor compounds in Huangjiu fermented with different wheat Qu[J].Food and Fermentation Industries, 2020, 46(8):226-233.
[3] 谢广发. 黄酒酿造技术[M].第三版.北京:中国轻工业出版社, 2020.
XIE G F.Brewing Technology of Huangjiu[M].3th ed.Beijing:China Light Industry Press, 2020.
[4] 徐玲, 刘登峰, 徐保国.基于数字式Smith预估增量式PID黄酒发酵温度控制[J].制造业自动化, 2014,36(23):33-36;43.
XU L, LIU D F, XU B G.The temperature control of Chinese rice wine based on the digital smith predictor incremental PID[J].Manufacturing Automation, 2014,36(23):33-36;43.
[5] LIU D F, ZHANG H T, XU B G, et al.Influence of fermentation temperature and source of enzymes on enological characteristics of rice wine[J].Journal of the Institute of Brewing, 2014, 120(3):231-237.
[6] LIU D F, ZHANG H T, XU B G, et al.Development of a kinetic model structure for simultaneous saccharification and fermentation in rice wine production[J].Journal of the Institute of Brewing, 2015, 121(4):589-596.
[7] 刘登峰, 熊伟丽, 徐玲, 等.黄酒双边发酵过程的建模[J].系统仿真学报, 2014, 26(3):626-630;674.
LIU D F, XIONG W L, XU L, et al.Modeling and simulation of Nverhong rice wine pre-fermentation[J].Journal of System Simulation, 2014, 26(3):626-630;674.
[8] 宗原, 刘登峰, 刘以安.基于改进蚁狮优化算法的黄酒发酵过程模型的参数辨识[J].食品与发酵工业, 2021, 47(2):153-159.
ZONG Y, LIU D F, LIU Y A.Model parameter identification of rice wine fermentation process based on an improved ant lion algorithm[J].Food and Fermentation Industries, 2021, 47(2):153-159.
[9] JANG J S.ANFIS:Adaptive-network-based fuzzy inference system[J].IEEE Transactions on Systems, Man, and Cybernetics, 1993, 23(3):665-685.
[10] ZOUNEMAT-KERMANI M, TESHNEHLAB M.Using adaptive neuro-fuzzy inference system for hydrological time series prediction[J].Applied Soft Computing, 2008, 8(2):928-936.
[11] SHIHABUDHEEN K V, PILLAI G N.Recent advances in neuro-fuzzy system:A survey[J].Knowledge-Based Systems, 2018, 152:136-162.
[12] GOLDBERG D E.Genetic Algorithms[M].Pearson Education India, 2013.
[13] DAS S, SUGANTHAN P N.Differential evolution:A survey of the state-of-the-art[J].IEEE Transactions on Evolutionary Computation, 2010, 15(1):4-31.
[14] TANABE R, FUKUNAGA A.Success-history based parameter adaptation for differential evolution[C].2013 IEEE Congress on Evolutionary Computation.IEEE, 2013:71-78.
[15] EBERHART, SHI Y H.Particle swarm optimization:Developments, applications and resources[C].Proceedings of the 2001 Congress on Evolutionary Computation (IEEE Cat.No.01TH8546).IEEE, 2022, 1:81-86.
[16] SALIMI H.Stochastic fractal search:A powerful metaheuristic algorithm[J].Knowledge-Based Systems, 2015, 75:1-18.
[17] MIRJALILI S, LEWIS A.The whale optimization algorithm[J].Advances in Engineering Software, 2016, 95:51-67
[18] JAIN M, SINGH V, RANI A.A novel nature-inspired algorithm for optimization:Squirrel search algorithm[J].Swarm and Evolutionary Computation, 2019, 44:148-175.
[19] ABDOLLAHZADEH B, GHAREHCHOPOGH F S, MIRJALILI S.African vultures optimization algorithm:A new nature-inspired metaheuristic algorithm for global optimization problems[J].Computers &Industrial Engineering, 2021, 158:107408.
[20] YANG Q, CHEN W N, DA DENG J, et al.A level-based learning swarm optimizer for large-scale optimization[J].IEEE Transactions on Evolutionary Computation, 2017, 22(4):578-594.
[21] TAKAGI T, SUGENO M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Transactions on Systems, Man, and Cybernetics, 1985, (1):116-132.
[22] CHEGINI S N, BAGHERI A, NAJAFI F.PSOSCALF:A new hybrid PSO based on sine cosine algorithm and levy flight for solving optimization problems[J].Applied Soft Computing, 2018, 73:697-726.