奶粉因其优异的功能特性和营养价值在食品工业中得到了广泛的应用,而大多数食品应用都对奶粉的品质要求较高[1]。分散性是速溶全脂奶粉(instant whole milk powder, IWMP)的重要品质性能之一[2],主要用于衡量奶粉粉末分解成单个奶粉颗粒的速度。此外,分散性是速溶全脂奶粉的一个关键特性,并对奶粉的复水性有重大影响[3]。目前,针对奶粉分散性的研究采用的方法有很多。例如,LEE等[4]利用水和空气的电阻差来获得奶粉的分散性,DAVENEL等[5]利用一种动态脉冲核磁共振(nuclear magnetic resonance, NMR)的方法测试奶粉的分散性。此外,有研究介绍了国际乳品联合会(International Dairy Federation,IDF)制定的一项测量分散性的标准方法。然而,由于这些方法既复杂又耗时,以至于实时检测奶粉的分散性仍是奶粉厂面临的一大挑战[6]。针对这个问题,DING等[7]利用速溶全脂奶粉的粒径和形状因子建立了奶粉分散性和容重的预测模型,这种简单的方法为进一步开发可以实时检测速溶全脂奶粉分散性和容重的在线检测技术提供了参考。
理想情况下,奶粉的重构是一个完整、快速的过程,是消费者所期望的重要功能特性。然而,当速溶全脂奶粉在水中重组时,总会存在一些未分散或未溶解的残留物。缓慢溶解颗粒(slowly dissolving particles, SDP)测试是一种观察奶粉在重构后残留在试管上颗粒的测量方法,也是一种溶解性能的评估[8]。该测试通常在乳制品行业中用于对速溶全脂奶粉的溶解性能进行分级[9]。MCKENNA等[10]指出缓慢溶解颗粒具有与粉末颗粒相似的结构,其缓慢溶解的现象是由表面组成或团聚体结构引起的。而TOIKKANEN等[11]则提出,这些不溶性颗粒的直径为几百微米,这些颗粒很可能具有不同于其他粉末颗粒的结构和组成。此外,LLOYD等[9]设计了一种图像分析方法,可以量化复原乳中悬浮的未溶解颗粒的数量,结果发现存在2种不同的缓慢溶解颗粒:体颗粒和表面颗粒。此外,利用缓慢溶解颗粒对奶粉的溶解性进行等级划分是一个主观过程,因为这个过程可能受到视力、光照等多种因素的影响。因此,开发一种软测量技术来预测奶粉溶解性能的等级是非常必要的。
影响速溶全脂奶粉分散性和溶解性的因素有很多。GAIANI等[12]与BOIARKINA等[13]指出奶粉颗粒的形态会影响奶粉的分散性,还提出了奶粉颗粒的形态会影响速溶全脂奶粉的溶解过程。另外,形状越不规则、直径越大的奶粉颗粒的分散性越好[14]。DING等[7]通过实验证明,颗粒大小和形态是影响速溶全脂奶粉分散性的重要因素之一。此外,有研究指出,奶粉颗粒的团聚是影响奶粉分散性和溶解性的关键因素[15],并受到奶粉工厂生产奶粉时的加工条件的影响[8]。CROWLEY等[3]提出,奶粉的加工条件比如温度、流速等,会影响奶粉的分散性和溶解性。![]() 同样发现了奶粉的溶解性与加工条件有关,尤其是流化床内的流化速度、雾化压力和出口处干燥空气的温度。
同样发现了奶粉的溶解性与加工条件有关,尤其是流化床内的流化速度、雾化压力和出口处干燥空气的温度。
不同奶粉企业的设施、生产环境、过程控制方案等因素各不相同,会造成品质检测不合格的可能性也不相同[6]。此外,传统的奶粉品质检测方法是一种耗时的离线检测方法,且由于这种方法的迟滞性,当因加工条件不当而产生的不合格奶粉产品被检测出来前,已经有大量的不合格奶粉产品被生产出来[16]。针对以上问题,本研究的目的是开发可以实时检测奶粉品质性能的在线软测量模型,以便及时地回收不合格奶粉产品,并通过调整加工条件生产出更优质的奶粉产品。本研究对某奶粉企业提供的35个奶粉样品进行了研究,同时该企业还提供了生产奶粉样品时的加工条件数据和所有奶粉样品的分散性和溶解性等级。首先,利用光学数码显微镜结合图像处理技术获取奶粉颗粒的形态特征参数。随后,利用重采样技术解决工厂原始数据中常见的不平衡数据集的问题。最后,利用重采样数据建立了2个偏最小二乘(partial least squares, PLS)模型和2个人工神经网络(artificial neural networks, ANN)模型,用于评估开发在线软测量技术来预测速溶全脂奶粉的分散性和溶解性的可行性。
1 材料与方法
1.1 奶粉样品制备
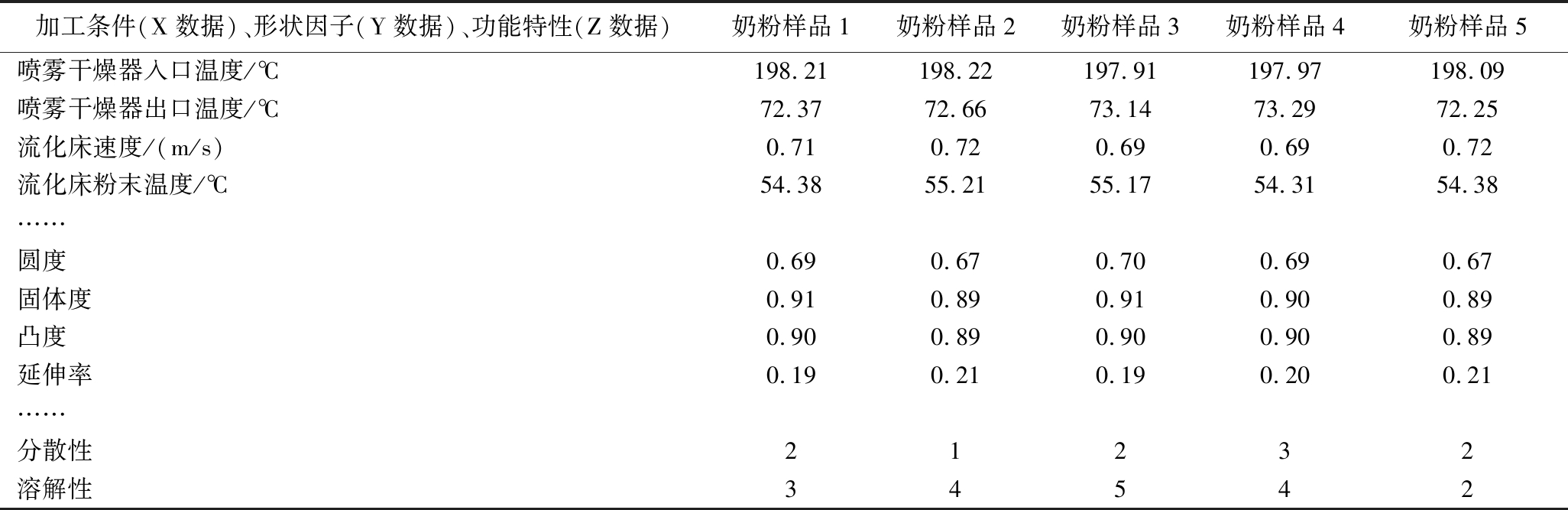
本文以某奶粉企业生产的35个速溶全脂奶粉样品为研究对象。利用加工条件参数和形状因子变量建立人工智能预测模型,预测速溶全脂奶粉的分散性和溶解性,如图1所示。由图1可以看出,该方法包括3种不同类型的工业测量数据(X,Y,Z数据)。X数据由标准工业传感器测得,包括喷嘴压力、干燥器入口空气温度、干燥器出口空气温度、流化床速度、流化床粉末温度等24个关键加工条件参数,Y数据包括圆形度、凸度、面积等9个奶粉颗粒形状因子变量,Z数据包括奶粉样品的2个重要功能特性(分散性和溶解性)。表1列出了其中几个奶粉样品的部分加工条件(X数据)、形状因子(Y数据)和功能特性(Z数据)。其中,所有的加工条件数据和功能特性数据都由奶粉工厂直接提供,而这2个功能特性的检测结果是由工厂技术人员通过特殊的检测方法测试所得,他们使用的测试类似于标准的IDF分散性测试[6],并根据工厂的要求以及经验划分而得的分类等级。而奶粉颗粒的形状因子是通过实验和计算所得。
表1 几个奶粉样品的部分加工条件(X数据)、形状因子(Y数据)和功能特性(Z数据)
Table 1 Partial processing conditions (X data), shape factors (Y data) and functional properties (Z data) of several milk powder samples
加工条件(X数据)、形状因子(Y数据)、功能特性(Z数据)奶粉样品1奶粉样品2奶粉样品3奶粉样品4奶粉样品5喷雾干燥器入口温度/℃198.21198.22197.91197.97198.09喷雾干燥器出口温度/℃72.3772.6673.1473.2972.25流化床速度/(m/s)0.710.720.690.690.72流化床粉末温度/℃54.3855.2155.1754.3154.38……圆度0.690.670.700.690.67固体度0.910.890.910.900.89凸度0.900.890.900.900.89延伸率0.190.210.190.200.21……分散性21232溶解性34542
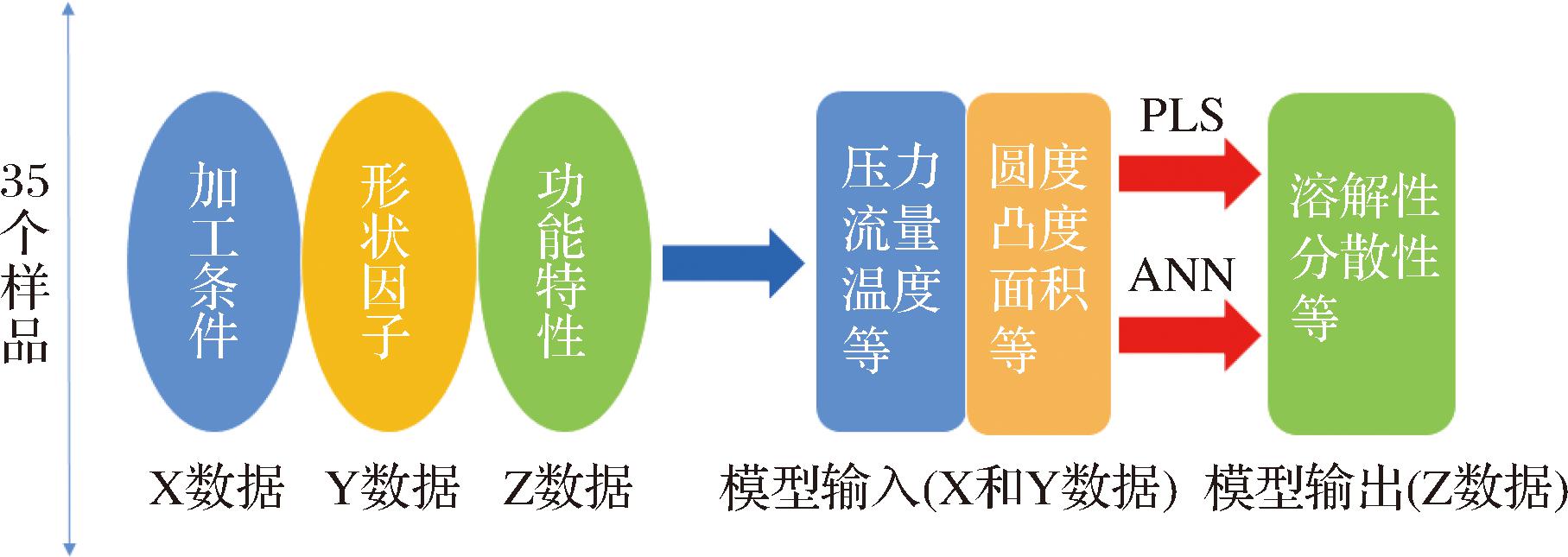
图1 利用3个数据集构建奶粉分散性和溶解性的人工智能预测模型
Fig.1 Constructing an artificial intelligence prediction model for milk powder dispersibility and solubility using three datasets
DEPREE等[6]研究了来自恒天然3个不同工厂、跨越6个季度的数千份奶粉样本数据,并利用工厂提供的所有加工条件数据构建了预测速溶全脂奶粉溶解性的偏最小二乘模型和人工神经网络模型,以及预测速溶全脂奶粉分散性的偏最小二乘模型,但是模型的预测结果并不理想。而本研究中所用的35个奶粉样品以及生产数据也均来自这3个恒天然工厂中的一个工厂,并且本研究利用工厂所提供的加工条件数据结合奶粉颗粒形状因子变量构建了可以预测奶粉溶解性和分散性的偏最小二乘和人工神经网络模型,以期提高模型的预测准确性。图2给出了利用工厂提供的全部(24个)加工条件参数区分不同工厂的奶粉样品的主成分分析得分图。由于奶粉样品数量庞大(既包含DEPREE等[6]研究的奶粉样品又包含本文中研究的所有奶粉样品),图中仅展示了部分奶粉样品。图2中,红色点为工厂1生产的奶粉样品,绿色点代表工厂2生产的奶粉样品,淡蓝色点为工厂3生产的奶粉样品,而本研究中使用的奶粉样品为深蓝色点。由图2可以看出,不同工厂的生产条件不同,而本研究中使用的35个奶粉样品(深蓝色点)都是由工厂2所生产的。
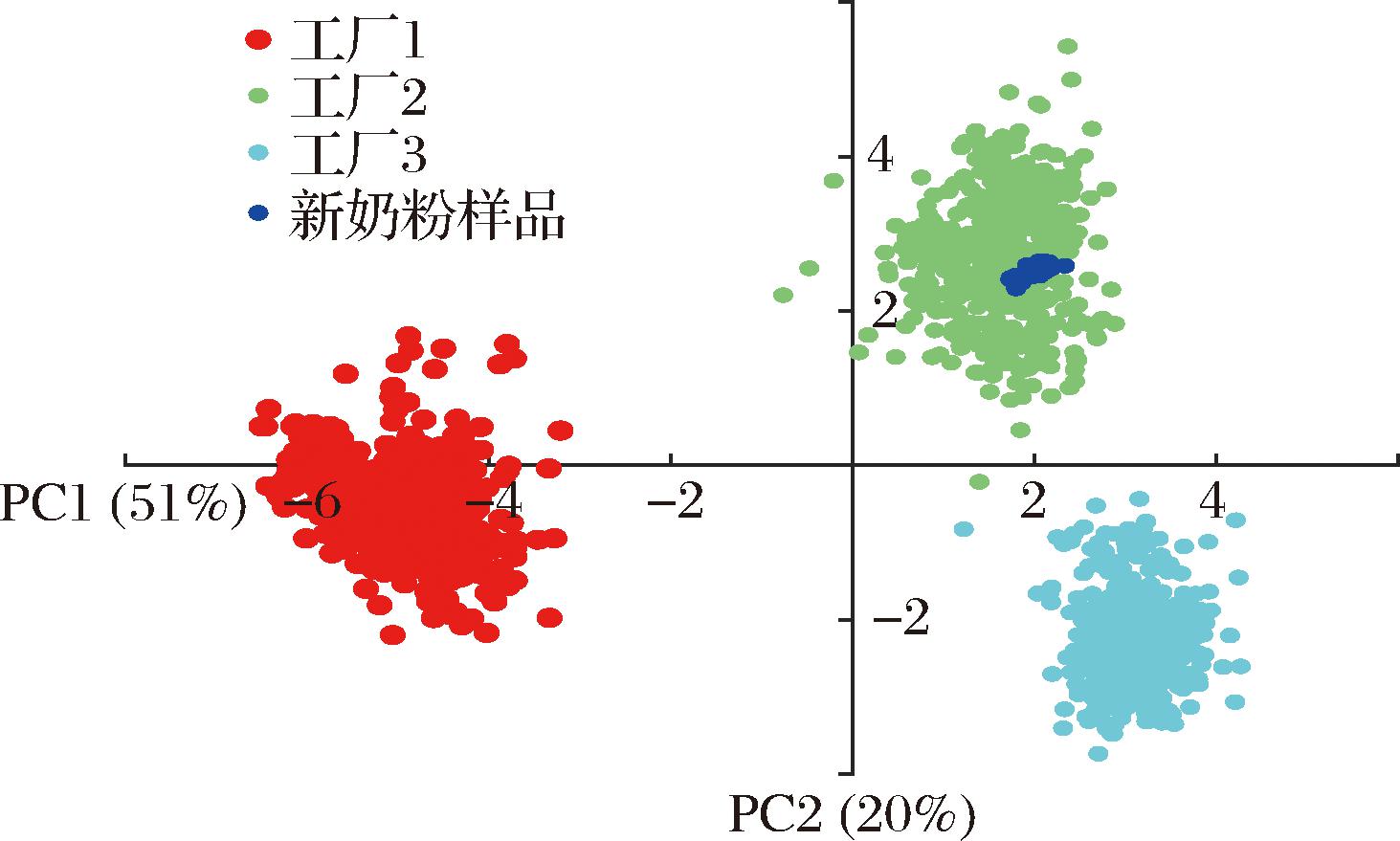
图2 利用加工条件数据构建不同奶粉厂家的主成分分析图
Fig.2 Constructing principal component analysis plots for different milk powder manufacturers using data on processing conditions
1.2 图像处理与形状因子
利用光学数码显微镜和图像处理技术相结合的方法,得到奶粉颗粒的形状因子。首先,将0.08 g奶粉样品放入16 mL菜籽油中。然后,用磁力搅拌器将混合液搅拌10 s。随后,利用移液器将1 mL混合液转移到显微镜载玻片上。使用光学数码显微镜(包含一个10倍物镜、一个10倍目镜和一个相机)为每个奶粉样本拍摄照片。最后,通过自定义的MATLAB函数对照片进行处理,计算并提取奶粉颗粒的边界。DING等[17]总结了图像处理的详细步骤。随后,用提取的边界计算出每个奶粉颗粒的形状因子。本研究计算的二维形状因子包括固体度、凹凸度、延伸率、圆形度、直径、面积、周长、最小Feret直径和最大Feret直径。图3展示了这些形状因子的详细信息,而DING等[7]总结了这些形状因子的详细定义。
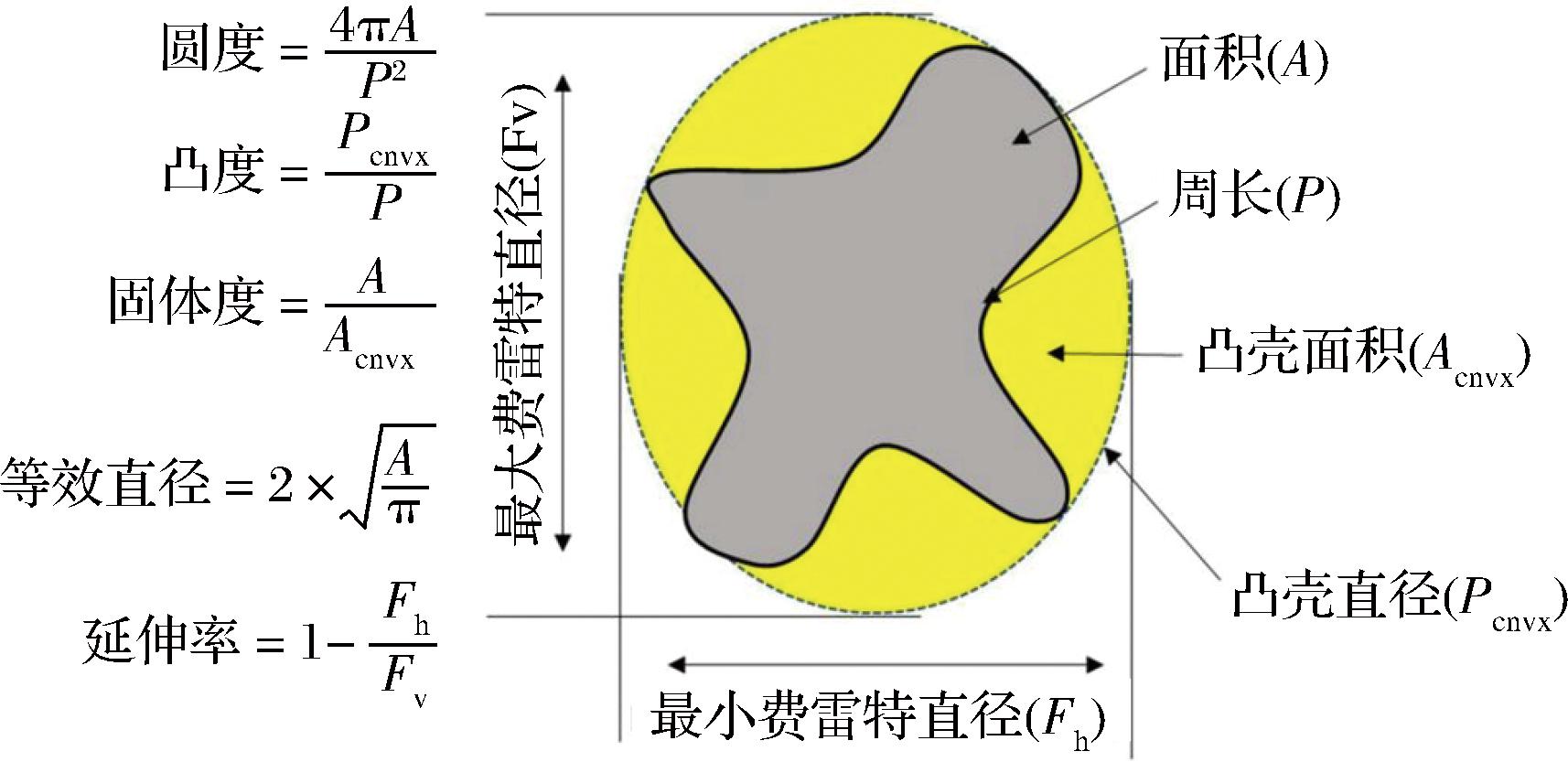
图3 形状因子的详细信息
Fig.3 Detailed information on shape factors
1.3 重采样
重采样是一种能够有效提高多变量模型预测能力的方法,它通过从初始样本中重复抽样,增加少数类数据集的数量[18]。采用这种方法,可以使少数类数据集的频率与其他数据集保持在相似的规模。
类别不平衡是生产数据中普遍存在的问题,过去的研究主要关注二元分类问题。其中一个关键问题是类内部的不平衡。为了解决这个问题,NICKERSON等[19]采用聚类的方法来识别类内的不平衡,然后对数据集进行重采样,以保持每个类内子集的相对密度。BATISTA等[20]也尝试了一些不同的方法对不平衡数据进行重采样,以建立决策树模型。然而,研究发现,与其他更复杂的方法相比,采用简单随机过采样方法所增加的复杂度最小,从而具有较强的竞争力。此外,DEPREE等[6]比较了利用来自工厂的原始不平衡数据集和重采样数据集(采用简单随机过采样方法处理不平衡数据集)进行建模,结果表明,基于重采样数据集建立的模型比基于不平衡数据集建立的模型更为可靠。因此,在本研究中,采用简单上采样(有放回的抽样)和随机下采样(减少多数类)来获得平衡的数据集。
1.4 数学建模与分析方法
1.4.1 偏最小二乘回归(PLS)
PLS是一种结构方程建模方法,能够最大化自变量对因变量方差的解释比例[21]。PLS模型已广泛应用于粒子分析领域[12,22-23]。本研究采用偏最小二乘法,利用速溶全脂奶粉的加工条件数据和形态参数变量,预测奶粉样品的溶解性和分散性。为了避免模型的过拟合,通过交叉验证来确定PLS分量的数量。对于奶粉样品的溶解性数据,重采样数据集有60个样本,而奶粉样品分散性的重采样数据集有45个样本。这些重采样的数据集被划分为5组,每组分别包含12个和9个样本。通过公式(1)和公式(2)计算这些PLS模型的多重相关系数R2(多重相关系数)和Q2(交叉验证的R2):
(1)
(2)
式中:PRESS表示所选数据的预测值和实际值之差的平方和;SS是Y的平均值和实际值之差的平方和;RSS表示拟合残差的平方和。
1.4.2 人工神经网络(ANN)
ANN是一种仿生计算体系,旨在模拟生物神经网络中的决策过程[24]。神经网络模型种类繁多,因其在处理非线性问题上的优秀表现,已被广泛应用于预测、控制和分类等领域。在本研究中,我们使用MATLAB的神经网络拟合工具,对各数据集进行神经网络模型训练,并对结果进行了比较。人工神经网络模型采用了带有Sigmoid隐藏神经元和线性输出层神经元的两层前馈网络,这些模型使用了Levenberg-Marquardt优化算法,虽然需要交大的内存空间,但却可以缩短模型训练时间[25]。此外,人工神经网络模型被划分为3个子集:训练集(占样本总数的70%)、验证集(占样本总数的15%)以及测试集(占样本总数的15%)。在确定隐藏层神经元数目方面,不同数量的隐藏神经元被尝试,并发现15个隐藏层神经元的效果最优。最后,为防止过度拟合,当验证误差达到最小值时,训练自动停止。
1.4.3 混淆矩阵
混淆矩阵[26]是一种评估分类器性能的有效工具,在数据分析、统计学和人工智能等领域得到了广泛的应用。在本研究中,利用混淆矩阵的精确率(accuracy)、特异性(specificity)和灵敏度(sensitivity)来评估和验证模型的性能。其中,精确率表示在整个数据集上的正确预测率,灵敏度是正确预测的样本占每个观察类别中样本总数的比率,而特异性则代表正确预测的样本占每个预测类别中样本总数的比率。
2 结果与分析
2.1 不平衡数据的重采样
对数据集进行重采样是生成具有实用预测性模型的关键步骤。本节将首先展示使用重采样数据集构建的PLS模型,随后是使用相同重采样数据集构建的ANN模型。图4显示了原始和重采样后的溶解性和分散性数据集的直方图。如图4-a所示,溶解性数据集展示了明显的重采样需求,其大部分数据集中在“3”和“4”类,而“2”和“5”类的样本相对较少,然而这两类是最值得预测的对象。图4-a中的原始数据集包含35个样本,经过重采样后每个类别都包含15个样本。如图4-b所示,用于预测分散性的原始数据集包含35个样本,而重采样后的数据集包含45个样本。重采样采用了随机抽样的方法,对数据多的类别进行下采样,对数据少的类别进行上采样,重采样后每个类别各含15个样本。
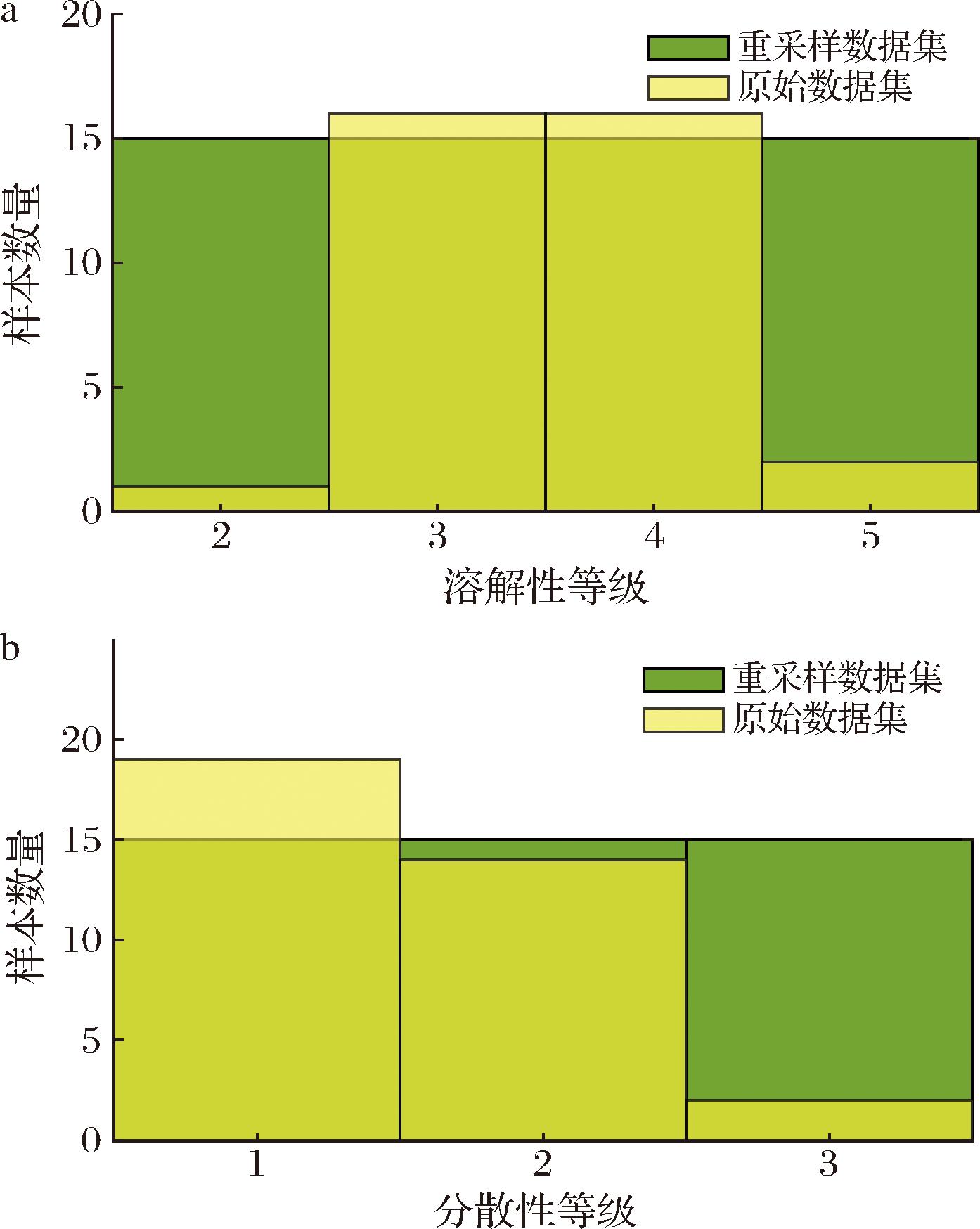
a-原始和重采样的溶解性数据集的直方图;b-原始和重采样分散性数据集的直方图
图4 原始和重采样的溶解性与分解性数据集的直方图
Fig.4 Histograms of original and resampled solubility and decomposability datasets
2.2 偏最小二乘模型
为了探究加工条件参数和形状因子变量是否能有效预测速溶全脂奶粉的溶解性和分散性,使用自定义的MATLAB函数对重采样数据构建了2个偏最小二乘模型。用于预测速溶全脂奶粉的溶解性和和分散性的输入数据是来自奶粉工厂的24个加工条件数据和奶粉样品的9个形状因子变量。
2.2.1 溶解性
第一个偏最小二乘模型利用加工条件数据和形状因子变量对速溶全脂奶粉的溶解性进行预测,并使用重采样数据集。图5展示了该模型的性能。其中,图5-a展示了R2和Q2与第一偏最小二乘模型的分量数的关系。R2和Q2的计算参照公式(1)和公式(2)。结果显示,当偏最小二乘模型的分量数为9时,Q2达到最大值(0.72),R2约为0.94。图5-b展示了在偏最小二乘模型有9个分量时,溶解性的预测值与观察值的对比。图中,溶解性的预测值和观察值为2、3、4、5四个等级(依次为优、良、合格、不合格)。此外,由于利用重复值对数据集进行了重采样,重采样的数据结果会在图中重叠在一起。因此,在观察值(x轴)中添加了一些噪声(均值为0,方差为0.1),以更好地区分数据点并显示数据分布。
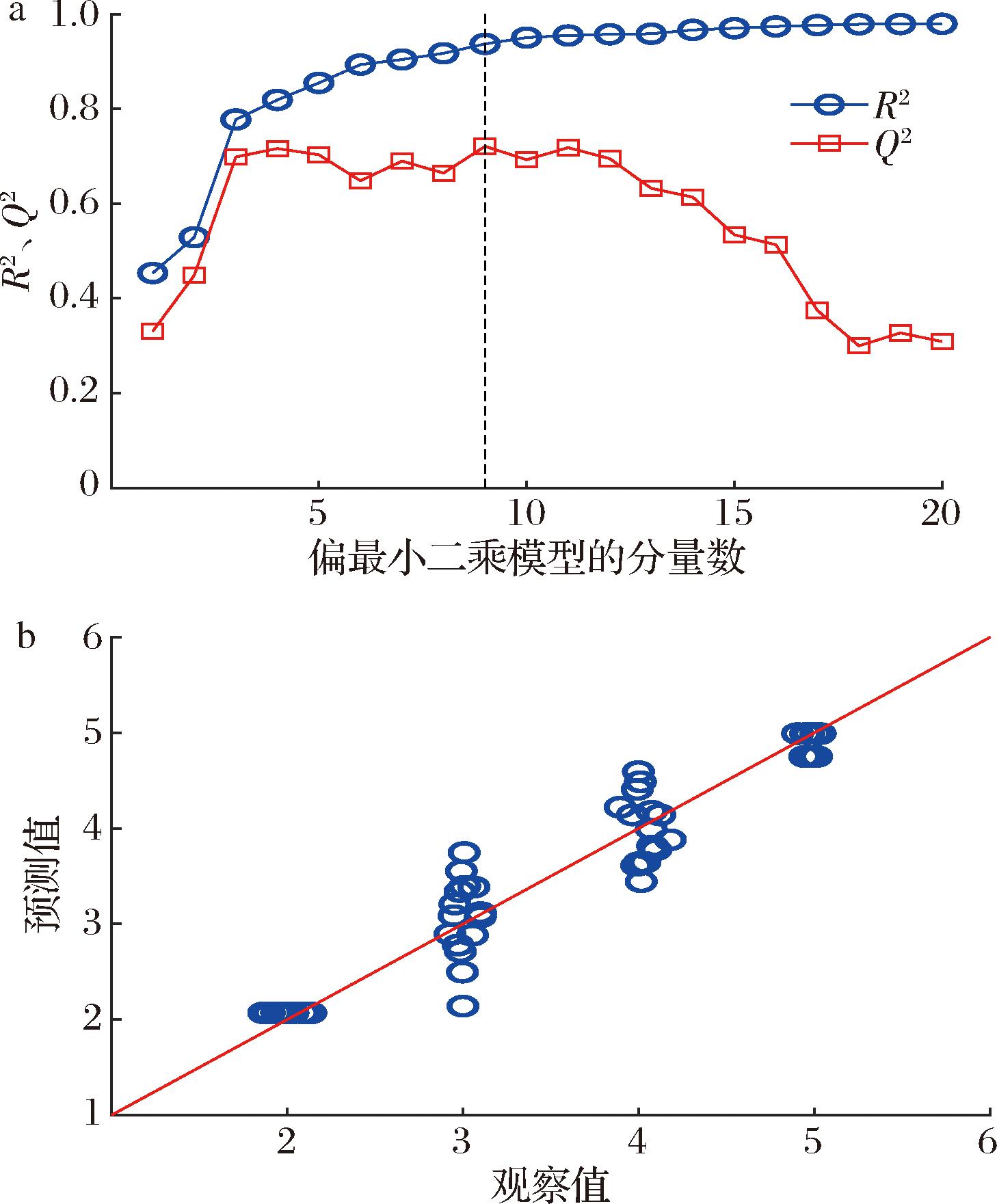
a-R2和Q2与第一个偏最小二乘模型的分量数的关系;b-溶解性的预测值与观察值的对比
图5 第一个偏最小二乘模型的性能图
Fig.5 Performance graph of the first partial least squares model
为了评估这个偏最小二乘模型的有效性,使用了原始的不平衡数据集进行测试。结果如图6所示,表2展示了该模型的混淆矩阵,包括精确率(accuracy,ACC)、特异性(specificity)和灵敏度(sensitivity)。35个原装奶粉样品被用于所构建的偏最小二乘模型的预测分析。在表2中,绿色部分表示预测的真阳性(TP)的数量,而假阴性(FN)和假阳性(FP)预测则被标为红色。从模型的结果可以看出,除了预测的第二类的特异性(0.333)相对较低外,大部分的灵敏度和特异性都相对较高,这可能是因为原始数据集是不平衡数据集,第二类只有1个样本。此外,模型的总体精确率为0.829。
表2 用于预测速溶全脂奶粉溶解性的偏最小二乘模型的混淆矩阵
Table 2 The confusion matrix of partial least squares model for predicting the solubility of instant whole milk powder
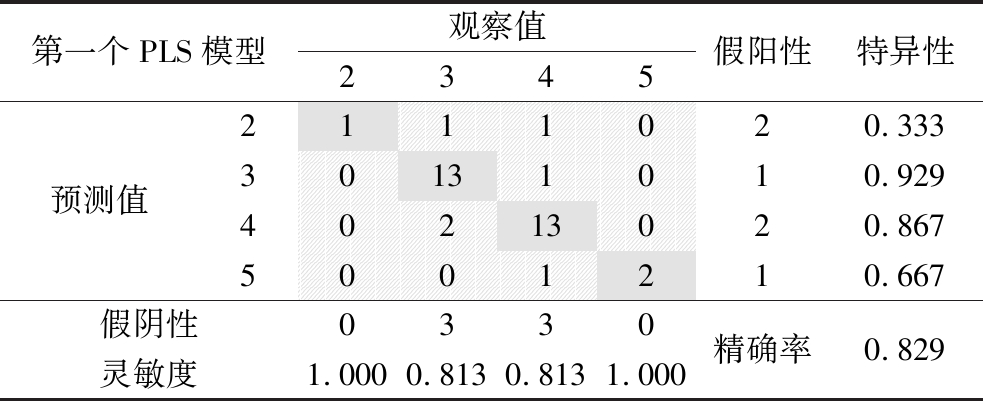
第一个PLS模型观察值2345假阳性特异性预测值2111020.33330131010.92940213020.8675001210.667假阴性0330精确率0.829灵敏度1.0000.8130.8131.000
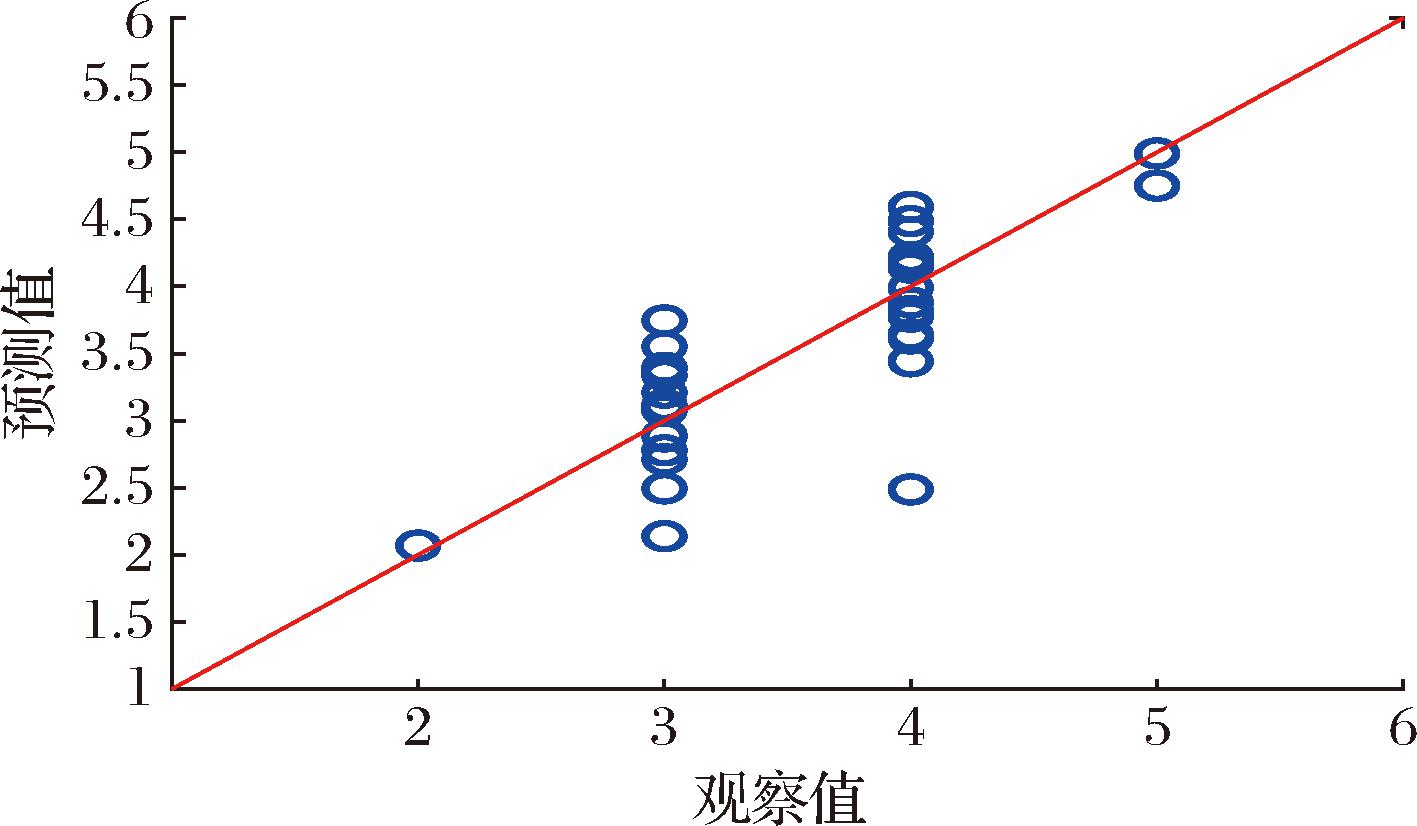
图6 使用原始的不平衡数据集对比偏最小二乘模型预测的溶解性与观察的溶解性
Fig.6 Comparing the predicted solubility of partial least squares models with the observed solubility using the original imbalanced dataset
2.2.2 分散性
第二个偏最小二乘模型是利用重采样的数据集来预测速溶全脂奶粉的分散性。图7-a展示了R2和Q2随偏最小二乘法分量数增加的变化。由图7-a可以看出,当模型包含10个分量时,模型的结果最好,此时Q2约为0.85,R2约为0.95。图7-b则比较了分散性的预测值和观察值。图中,分散性的预测值和观察值为1、2、3三个等级(依次为优、合格、不合格)。此外,由于同样利用重复值对数据集进行了重采样,重采样的数据结果会在图中重叠在一起。因此,同样在图7-b的观测值中添加了一些噪声(均值为0,方差为0.1),以更好地区分数据点并显示数据分布。
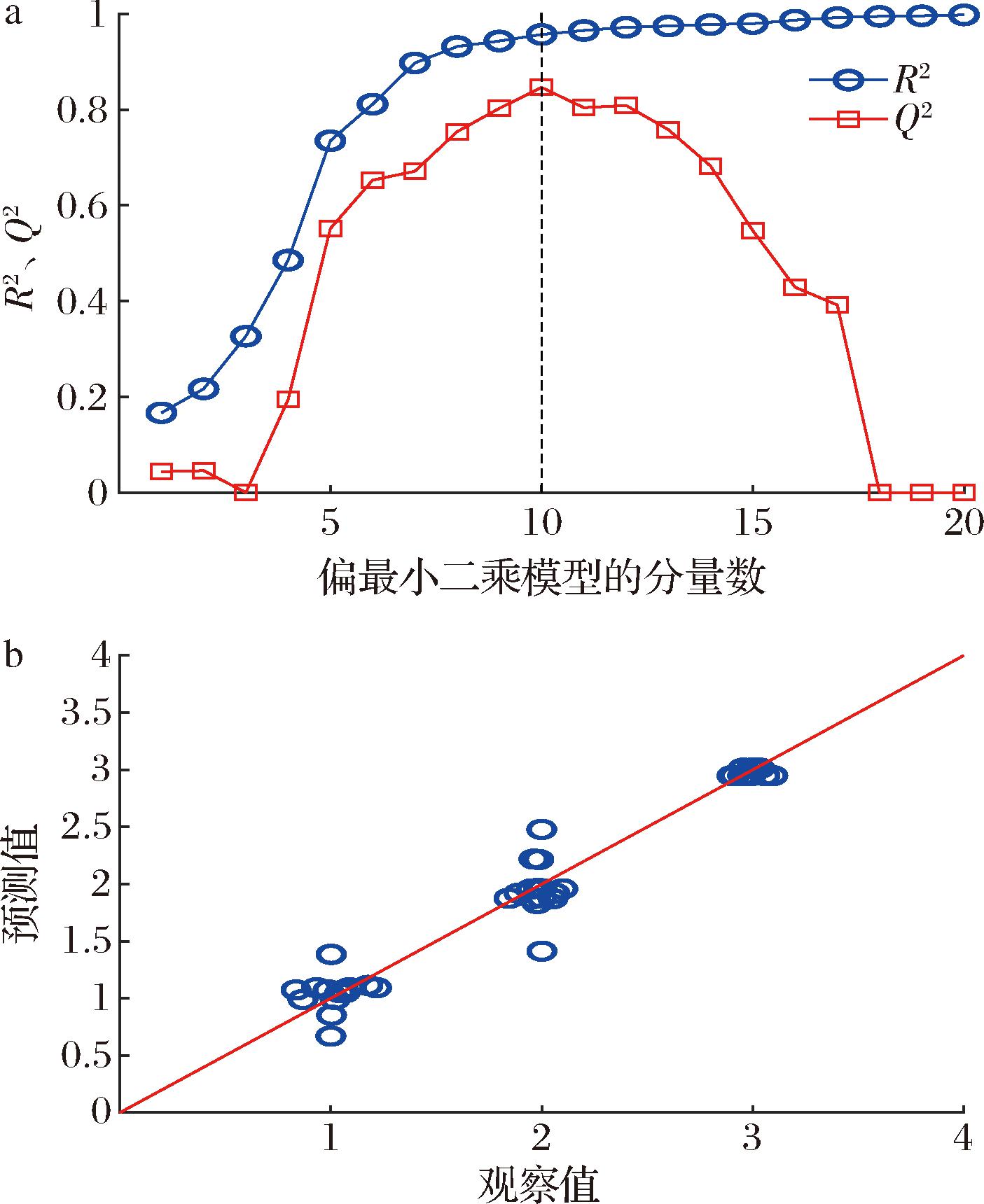
a-R2和Q2与第一个偏最小二乘模型的分量数的关系;b-分散性的预测值与观察值的对比
图7 第二个偏最小二乘模型的性能图
Fig.7 Performance graph of the second partial least squares model
用35个原始奶粉样品数据对构建的第二个偏最小二乘模型进行了验证。图8展示了这个验证模型的分散性的预测值与观察值的对比,表3则给出了这个验证模型的混淆矩阵的结果。与前一个混淆矩阵相似,绿色部分表示真阳性(TP)预测,而红色部分则代表假阳性(FP)和假阴性(FN)预测。由表3可以看出,所构建的第二个偏最小二乘模型的精确度约为0.743。从模型的结果可以看出,所构建的2个偏最小二乘模型在预测速溶全脂奶粉的溶解性和分散性方面表现较好(模型的R2约为0.94和0.95,验证模型的精度约为0.829和0.743)。
表3 验证偏最小二乘模型的混淆矩阵
Table 3 Verifying the confusion matrix of partial least squares models
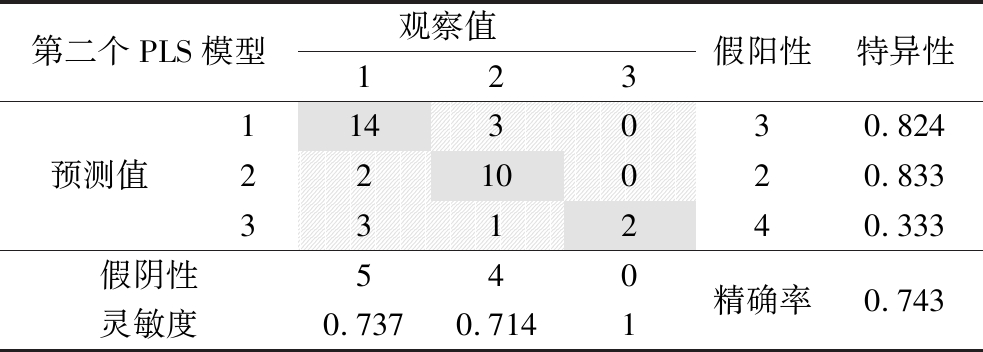
第二个PLS模型观察值123假阳性特异性预测值1143030.8242210020.833331240.333假阴性540精确率0.743灵敏度0.7370.7141
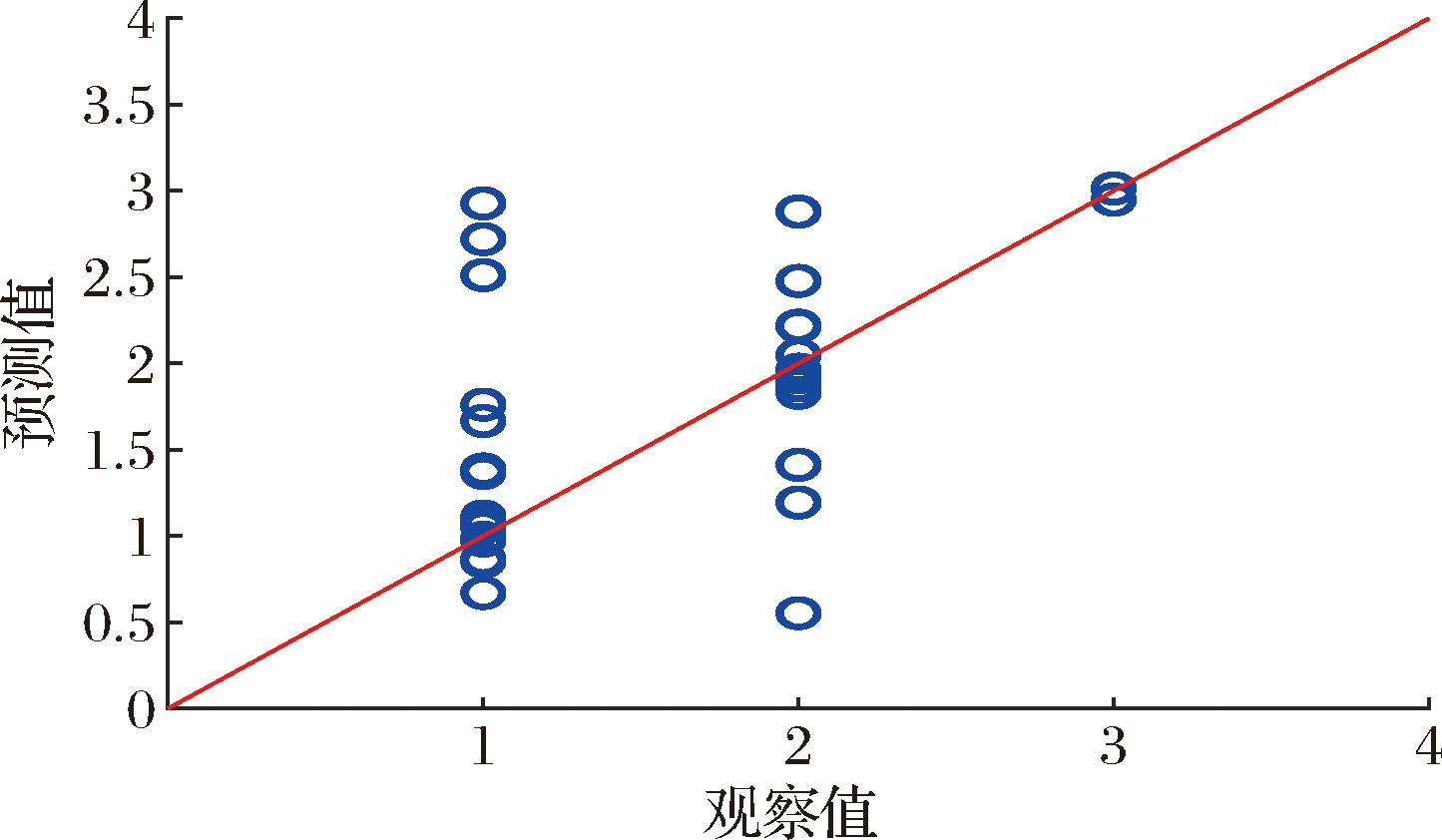
图8 使用原始不平衡数据集验证构建的偏最小二乘模型的分散性的预测值与观测值的对比
Fig.8 Comparison of predicted and observed values for the dispersion of the constructed partial least squares model using the original imbalanced dataset validation
2.3 人工神经网络模型
为了预测速溶全脂奶粉的溶解性和分散性,进一步建立了人工神经网络模型。在此模型中,同样使用了加工条件数据和形状因子变量,且使用了经过重采样的数据集,并利用了原始数据集和混淆矩阵来验证所构建模型的准确性。
2.3.1 溶解性
首先构建了一个用于预测速溶全脂奶粉溶解性的人工神经网络模型。所使用的重采样数据集包含60个奶粉样本,其中42个用于模型训练,9个用于模型验证,剩余的9个用于模型测试。图9-a展示了第一个人工神经网络模型的结果。由图9-a可以看出,当epoch(训练轮次)为3时,验证模型的均方误差达到最小值。因此,选用epoch为3的人工神经网络模型。图9-b展示了该人工神经网络模型的性能。同样在X轴上添加了一点噪声用于更好的区分数据点。此外,表4列出了该人工神经网络模型的结果。
表4 第一个用于预测速溶全脂奶粉溶解性的人工神经网络模型的结果
Table 4 Results of the first artificial neural network model for predicting the solubility of instant whole milk powder
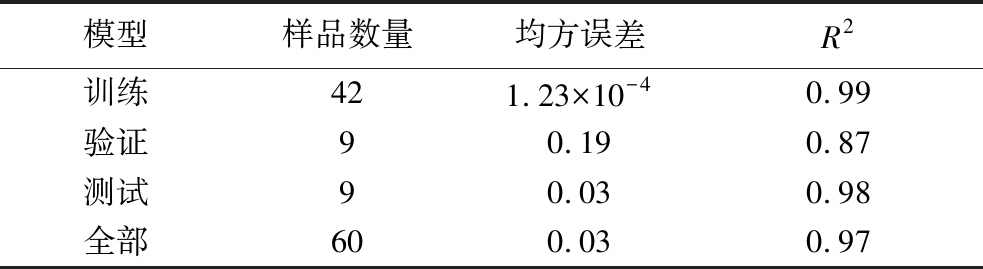
模型样品数量均方误差R2训练421.23×10-40.99验证90.190.87测试90.030.98全部600.030.97
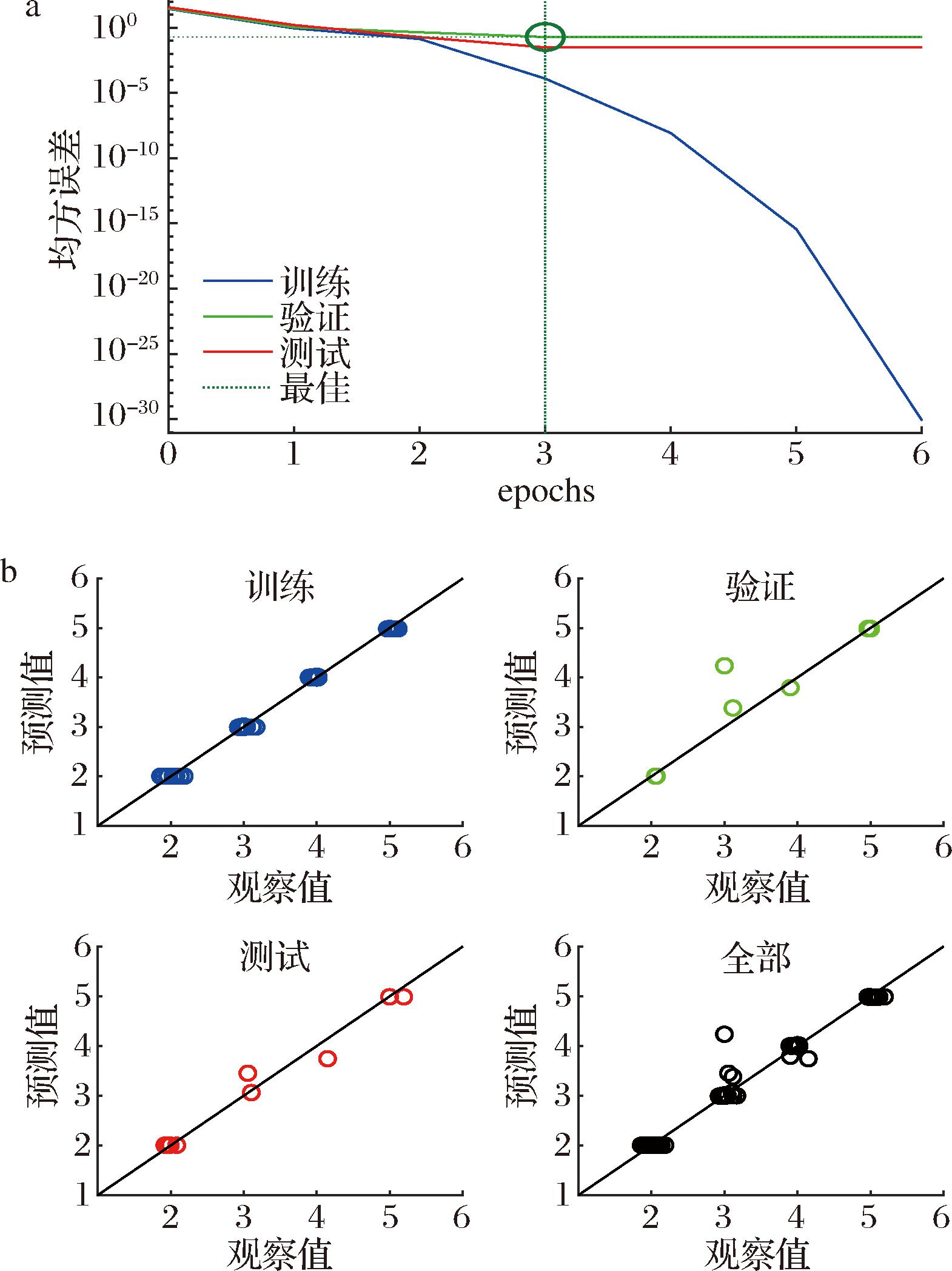
a-用于预测速溶全脂奶粉溶解性的第一个人工神经网络模型;b-第一个人工神经网络模型在预测速溶全脂奶粉溶解性方面的性能
图9 第一个人工神经网络模型的性能图
Fig.9 Performance graph of the first artificial neural network model
35个原始奶粉样品被用于评估这个人工神经网络模型的有效性。图10展示了验证的人工神经网络模型预测的溶解性与观察到的溶解性的对比,而表5列出了该人工神经网络模型的混淆矩阵。类似于之前的混淆矩阵,真阳性(TP)预测用绿色表示,假阳性(FP)和假阴性(FN)预测用红色表示。此外,该神经网络模型的准确性也在表5中列出。从模型的结果可以看出,验证的人工神经网络模型的特异性和灵敏度都高于第一个验证的偏最小二乘模型。此外,该模型的R2值为0.97,优于第一个偏最小二乘模型的R2值0.94。此外,该模型的精度(0.914)也高于第一个偏最小二乘模型的精度(0.829)。
表5 验证的人工神经网络模型的混淆矩阵
Table 5 The confusion matrix of the validated artificial neural network model
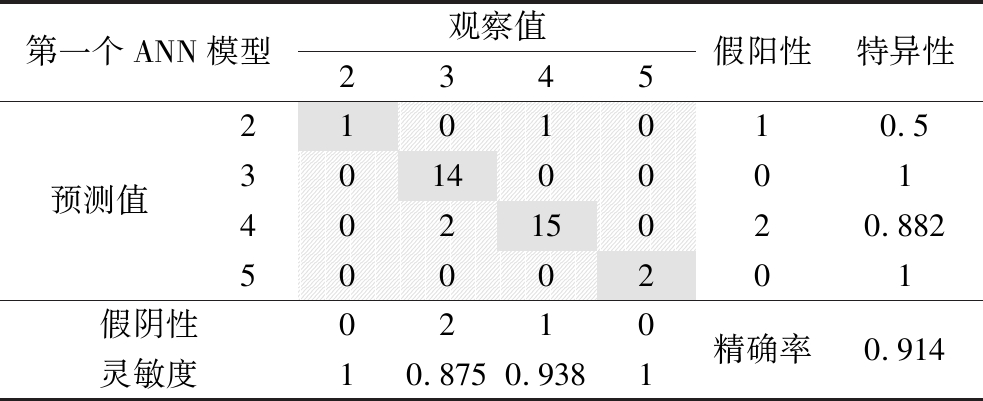
第一个ANN模型观察值2345假阳性特异性预测值2101010.53014000140215020.8825000201假阴性0210精确率0.914灵敏度10.8750.9381
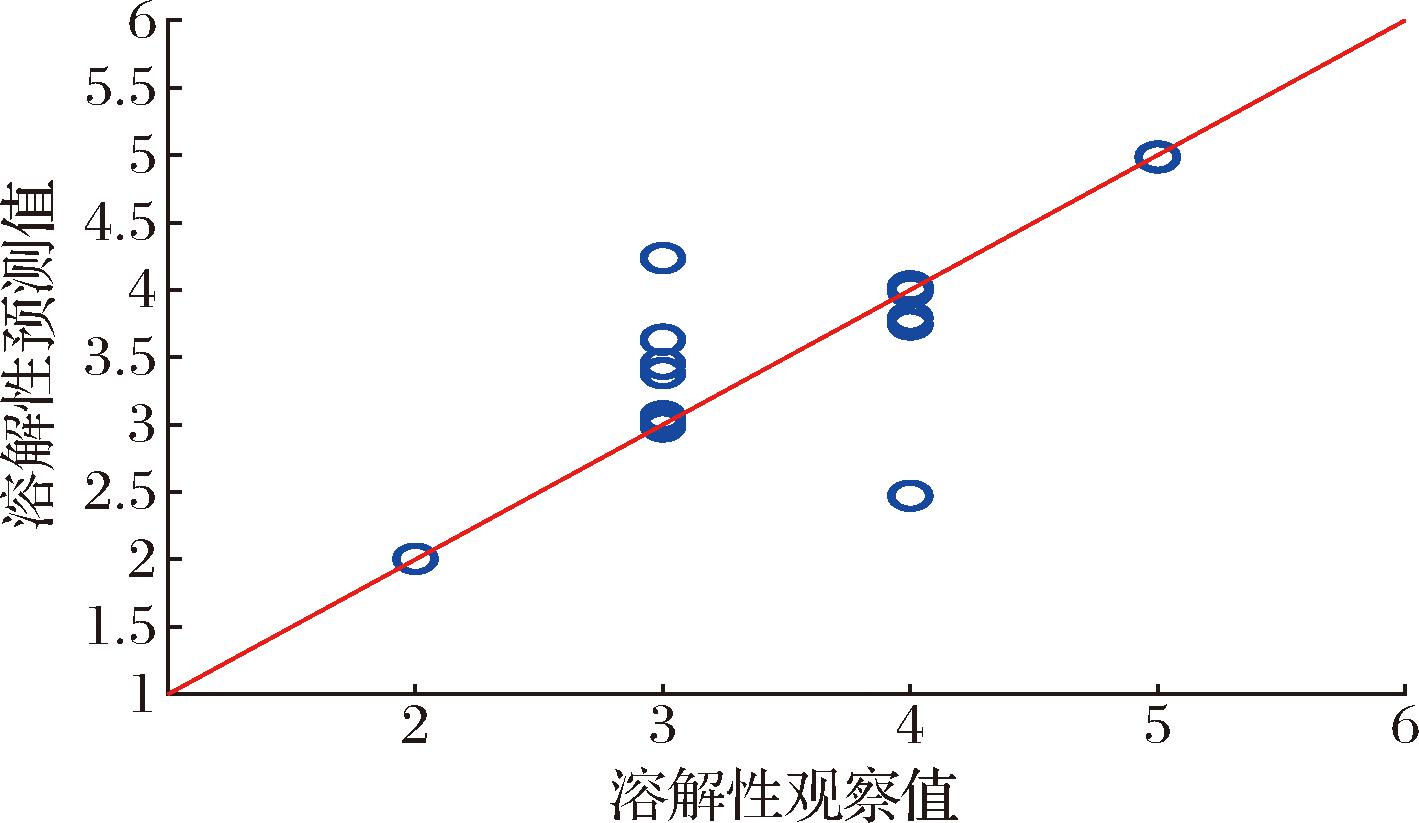
图10 使用原始不平衡数据集验证的人工神经网络模型预测的溶解性与观察的溶解性的对比
Fig.10 Comparison of predicted solubility and observed solubility using an artificial neural network model validated using raw imbalanced datasets
2.3.2 分散性
构建了第二个人工神经网络模型用于预测速溶全脂奶粉的分散性。图11-a展示了该模型的验证过程:在epoch为2时,验证模型的均方误差达到最低值。因此,epoch为2的人工神经网络模型被选用。此人工神经网络模型的训练样本有31个,验证样本有7个,测试样本也有7个。图11-b展示了该模型的性能,同样在观测值中添加了一些噪声。此外,表6列出了第二个人工神经网络模型的结果。
表6 第二个人工神经网络模型的预测结果
Table 6 Prediction results of the second artificial neural network model
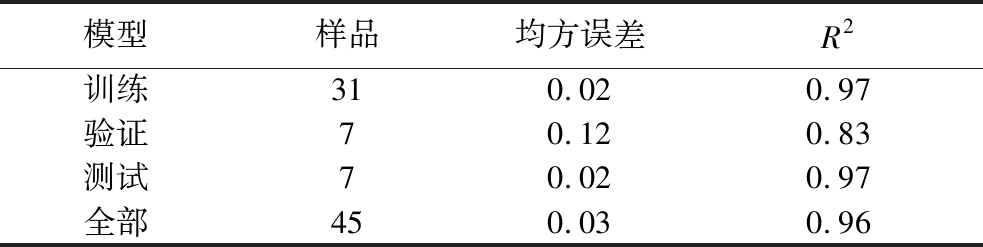
模型样品均方误差R2训练310.020.97验证70.120.83测试70.020.97全部450.030.96
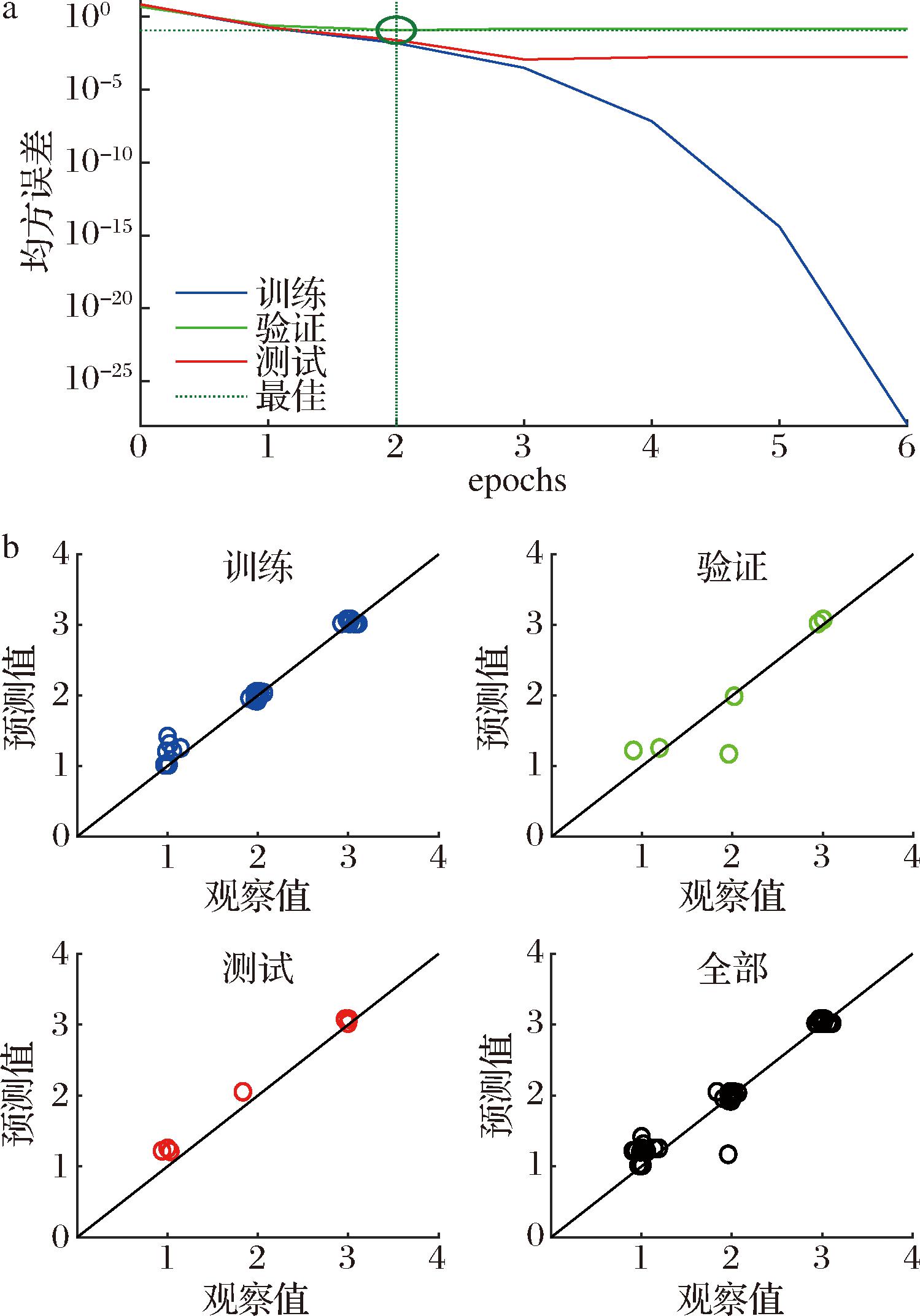
a-第二个人工神经网络模型的验证过程;b-第二个人工神经网络模型预测速溶全脂奶粉分散性的性能
图11 第二个人工神经网络模型的性能图
Fig.11 Performance graph of the second artificial neural network model
最后,使用35个原始奶粉样本对构建的第二个神经网络模型进行了验证。图12显示了验证的人工神经网络模型的预测分散性与观测分散性的对比,表7列出了该模型的混淆矩阵。真阳性(TP)预测用绿色表示,假阳性(FP)和假阴性(FN)预测用红色表示。该模型的总体精度也在表7中列出。结果显示,第二个人工神经网络模型预测速溶全脂奶粉分散性的R2值(0.96)略高于第二个偏最小二乘模型预测速溶全脂奶粉分散性的R2值(0.95),而这2个模型的精度均为0.743。
表7 验证人工神经网络模型的混淆矩阵
Table 7 Verifying the confusion matrix of artificial neural network models
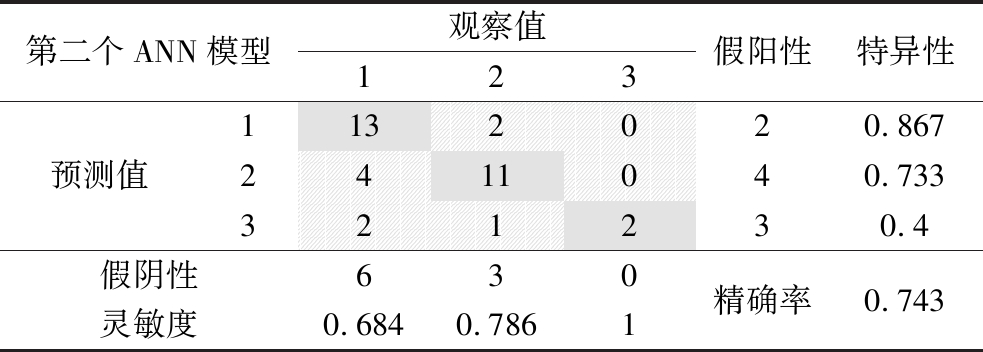
第二个ANN模型观察值123假阳性特异性预测值1132020.8672411040.733321230.4假阴性630精确率0.743灵敏度0.6840.7861
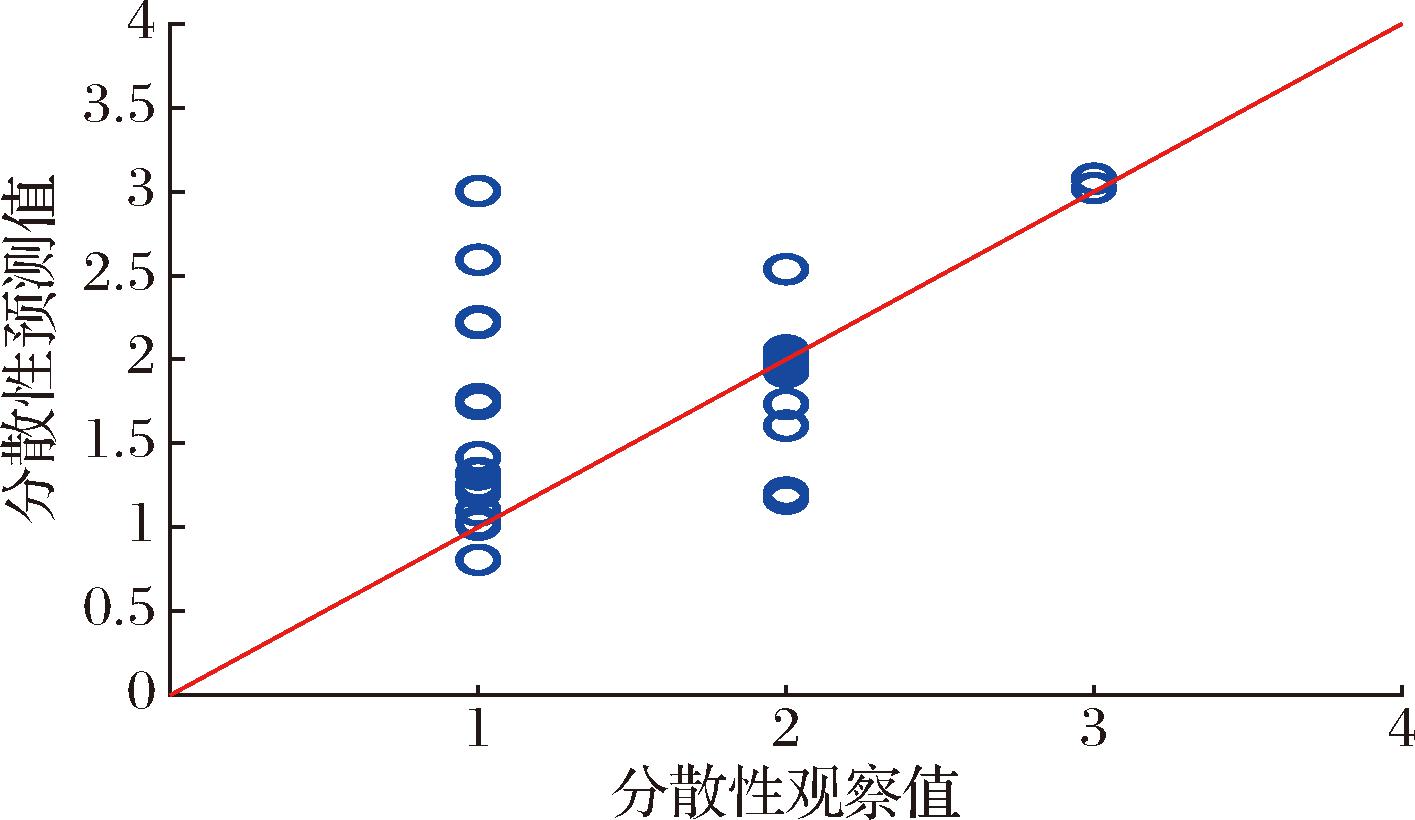
图12 使用原始不平衡数据集验证人工神经网络模型的预测分散性与观测分散性的对比
Fig.12 Comparison of predictive dispersion and observational dispersion of artificial neural network models verified with original unbalanced datasets
总的来说,相比于仅使用加工条件数据构建的模型[6],本研究的偏最小二乘模型和人工神经网络模型在预测溶解性上的R2值(分别为0.94和0.97)都明显高于之前模型的R2值(分别约为0.7和0.9),而本研究的偏最小二乘模型在预测分散性上的R2值(约为0.95)也明显高于之前模型的R2值(约为0.88)。此外,相较于仅使用形状因子变量构建的模型DING等[7],本研究的偏最小二乘模型和人工神经网络模型在预测分散性上的R2值(0.95和0.96)也明显优于之前模型的R2值(分别为0.47和0.81)。因此,结合加工条件数据和形状因子变量建立模型来预测速溶全脂奶粉的溶解性和分散性是可行的。然而,虽然构建的用于预测全脂速溶奶粉分散性的偏最小二乘模型和人工神经网络模型的R2值分别为0.95和0.96,但他们的验证模型的总体精确率均只有0.743。这可能是由于以下三点原因造成。首先,在对模型的数据集进行预处理(重采样)时,本研究使用了简单的重复上采样和随机下采样,特别是针对1类分散性,随机删除了其中部分数据使1类数据和其他两类数据的数据量保持平衡。而在验证模型的结果中可以看出,被删除的1类数据的预测结果均出现偏差。因此,建议在数据预处理时可以尝试其他的重采样方法,并且尽量使用上采样,以避免训练模型时没有将被删除数据的特征考虑到模型中。其次,本研究训练模型时选用的特征值为奶粉的9个形状参数和工厂提供的24个加工条件参数,可能还有其他的特征没有被纳入模型中。建议尝试纳入更多的特征值(比如更多奶粉的形状参数或工厂的加工条件参数)以提高模型的精确度。第三,本研究仅使用了35个奶粉样本,数据量不足可能会导致所构建模型出现过拟合现象,即模型在训练数据集上的性能很好,但在其他数据集上的性能却很差。建议可以获取更多的奶粉样本数据用于训练模型来提升模型的准确率。
此外,虽然人工神经网络模型的性能优于偏最小二乘模型,但目前的行业更倾向于选择偏最小二乘模型,这是因为人工神经网络模型是一个黑盒模型,而偏最小二乘模型可以直接将实际的加工条件数据和形状因子变量关联起来,从而找出哪些变量对速溶全脂奶粉的溶解性和分散性有较好的改善作用。
3 结论
本研究旨在通过探索加工条件参数和形状因子变量对速溶全脂奶粉的分散性能和溶解性能的影响,以便开发用于奶粉品质性能的软测量模型。此外,使用重采样方法解决工厂数据中不平衡数据集问题,这种问题会导致模型开发过程中最高和最低类别的样本不足,从而被模型忽略的问题。实际上,这些测试结果为不合格的奶粉样品对所构建的模型的预测是最有价值的,因为这些奶粉样品的错误预判可能会导致大量奶粉产品被降级处理或重新加工,从而增加材料的成本。在此基础上,本研究建立了2个偏最小二乘模型和2个人工神经网络模型,用于预测速溶全脂奶粉的溶解性和分散性。这些模型的良好性能表明了利用奶粉加工条件参数和形状因子变量开发在线软测量技术来预测速溶全脂奶粉的溶解性和分散性是可行的。此外,尽管人工神经网络模型的预测结果要优于偏最小二乘模型的预测结果,但由于黑盒模型的局限性以及偏最小二乘模型可以直接构建输入变量与输出变量之间的关系等优点,偏最小二乘模型更适合用于奶粉工厂来预测奶粉的各项品质性能。
[1] 赵爱利, 王文祥.到底哪个奶营养价值更高?[N].人民政协报, 2021-10-27(7).ZHAO A L, WANG W X.Which milk has higher nutritional value? [N].People′s Political Consultative Conference News, 2021-10-27(7).
[2] 袁永俊, 陈宝琳. 改善豆奶粉冲调性能的技术研究[J]. 四川工业学院学报, 1999(4):42-46.YUAN Y J, CHEN B L. Study on the technology for improving soybean milk powder's dissolution properties[J]. Journal of Sichuan University of Science and Technology, 1999(4):42-46.
[3] CROWLEY S V, DESAUTEL B, GAZI I, et al.Rehydration characteristics of milk protein concentrate powders[J].Journal of Food Engineering, 2015, 149:105-113.
[4] LEE J, CHAI C, PARK D J, et al.Novel convenient method to determine wettability and dispersibility of dairy powders[J].Korean Journal for Food Science of Animal Resources, 2014, 34(6):852.
[5] DAVENEL A, SCHUCK P, MARIETTE F, et al.NMR relaxometry as a non-invasive tool to characterize milk powders[J].Le Lait, 2002, 82(4):465-473.
[6] DEPREE N, PRINCE-PIKE A, YOUNG B, et al.Predictive modelling of instant whole milk powder functional performance across three industrial plants[J].Journal of Food Engineering, 2019, 252:1-9.
[7] DING H H, YU W, BOIARKINA I, et al.Effects of morphology on the dispersibility of instant whole milk powder[J].Journal of Food Engineering, 2020, 276:109841.
[8] ![]() J.Handbook of Milk Powder Manufacture[M].GEA Process Engineering A/S, 2012.
J.Handbook of Milk Powder Manufacture[M].GEA Process Engineering A/S, 2012.
[9] LLOYD R, STEWART H, BAILEY D.Slowly dissolving particles in instant whole milk powder-characterisation and quantitative analysis[J].International Dairy Journal, 2019, 97:65-70.[10] MCKENNA A B, LLOYD R J, MUNRO P A, et al.Microstructure of whole milk powder and of insolubles detected by powder functional testing[J].Scanning, 1999, 21(5):305-315.
[11] TOIKKANEN O, OUTINEN M, MALAFRONTE L, et al.Formation and structure of insoluble particles in reconstituted model infant formula powders[J].International Dairy Journal, 2018, 82:19-27.
[12] GAIANI C, BOYANOVA P, HUSSAIN R, et al.Morphological descriptors and colour as a tool to better understand rehydration properties of dairy powders[J].International Dairy Journal, 2011, 21(7):462-469.
[13] BOIARKINA I, YE J, PRINCE-PIKE A, et al. The morphology of instant whole milk powder from different industrial plants[C], Chemeca 2016: Chemical Engineering-Regeneration, Recovery and Reinvention. Melbourne: Engineers Australia, 2016: 945-953.
[14] SHARMA A, JANA A H, CHAVAN R S.Functionality of milk powders and milk-based powders for end use applications—A review[J].Comprehensive Reviews in Food science and Food safety, 2012, 11(5):518-528.
[15] DHANALAKSHMI K, GHOSAL S, BHATTACHARYA S.Agglomeration of food powder and applications[J].Critical reviews in food science and nutrition, 2011, 51(5):432-441.
[16] KHAN A, MUNIR M T, YU W, et al.Wavelength selection for rapid identification of different particle size fractions of milk powder using hyperspectral imaging[J].Sensors, 2020, 20(16):4645.
[17] DING H H, LI B, BOIARKINA I, et al.Effects of morphology on the bulk density of instant whole milk powder[J].Foods, 2020, 9(8):1024.
[18] 李昂, 韩萌, 穆栋梁, 等. 多类不平衡数据分类方法综述[J]. 计算机应用研究, 2022, 39(12):3534-3545.LI A, HAN M, MU D L, et al. Survey of multi-class imbalanced data classification methods[J]. Application Research of Computers, 2022, 39(12):3534-3545.
[19] NICKERSON A, JAPKOWiCZ N, MILIOS E E.Using unsupervised learning to guide resampling in imbalanced data sets[C].International Workshop on Artificial Intelligence and Statistics, 2001:224-228.
[20] BATISTA G E A P A, PRATI R C, MONARD M C.A study of the behavior of several methods for balancing machine learning training data[J].Acm Sigkdd Explorations Newsletter, 2004, 6(1):20-29.
[21] 尹延顺, 姜欣, 宋涛, 等. 基于偏最小二乘法分析复合型果酒风味成分与感官属性之间的相关性[J]. 食品与发酵工业, 2021, 47(22):234-240.YIN Y S, JIANG X, SONG T, et al. Correlation analysis on flavor compositions and sensory attributes of compound fruit wines based on partial least squares regression[J]. Food and Fermentation Industries, 2021, 47(22):234-240.
[22] ZHANG H, MIAO Y L, TAKAHASHI H, et al.Amylose analysis of rice flour using near-infrared spectroscopy with particle size compensation[J].Food Science and Technology Research, 2011, 17(4):361-367.
[23] MUNIR M T, WILSON D I, YU W, et al.An evaluation of hyperspectral imaging for characterising milk powders[J].Journal of Food Engineering, 2018, 221:1-10.
[24] 李冰, 郭祀远, 李琳, 等. 人工神经网络在食品工业中的应用[J]. 食品科学, 2003, 24(6):161-164.LI B, GUO S Y, LI L, et al. The processing of artificial neural network in food industry[J]. Food Science, 2003, 24(6):161-164.
[25] PIOTROWSKI A P, NAPIORKOWSKI J J.Optimizing neural networks for river flow forecasting-evolutionary computation methods versus the levenberg-marquardt approach[J].Journal of Hydrology, 2011, 407(1-4):12-27.
[26] 孔英会, 景美丽. 基于混淆矩阵和集成学习的分类方法研究[J]. 计算机工程与科学, 2012, 34(6):111-117.KONG Y H, JING M L. Research of the classification method based on confusion matrixes and ensemble learning[J]. Computer Engineering &Science, 2012, 34(6):111-117.