西兰花作为“果蔬皇后”,内含大量营养物质,但采后生命活动旺盛,新陈代谢仍然活跃,在常温下,极易发生黄化,发臭、腐败等品质下降的问题,在农业生产中,需全程冷链运输[1]。温度是冷链运输的核心,需在贮运过程中对果蔬实施连续且稳定的低温控制,过高的温度会加快果蔬腐败速度,其源头温度尤为重要[2]。因此果蔬采后常采用预冷作业,降低果蔬核心温度,再进行冷链运输,抑制果蔬在贮运过程中的生命活动,延长保鲜时间[3]。
目前常用的果蔬预冷方法包括压差预冷、冷库预冷、冰水预冷以及碎冰预冷等,存在着预冷时间长、能耗高、费时费工的问题[4]。流态冰具有流动性好、冷却速度快等特点,既满足了果蔬快速预冷的要求,又可保持贮运过程中较为稳定的低温,且有助于果蔬保持水分,在果蔬保鲜领域应用前景广阔[5]。刘瑶等[6-7]测试经流态冰处理后的西兰花和甜玉米的理化指标,发现流态冰可有效维持西兰花和甜玉米的贮藏品质。李翠红等[8]研究发现流态冰预冷近冰温贮藏西兰花的叶绿素含量、萝卜硫素含量、维生素C含量等营养物质均高于未处理的对照组。时文林[9]对比冷库预冷、压差预冷和流态冰预冷对甜玉米品质的影响,通过各项理化指标的测试,表明流态冰预冷在贮藏期间保鲜效果最佳。李淦等[10]通过计算流体动力学(computational fluid dynamics,CFD)模拟流态冰贮存西兰花过程中温度场和冰晶颗粒的变化,发现冰晶颗粒分布、流态冰体积分数对果蔬预冷的均匀性影响显著。孟维岩等[11]探究了甜玉米包装中果蔬排列对流态冰预冷效果的影响,发现甜玉米竖直放置更有利于甜玉米预冷。上述研究重点关注的是研究流态冰对果蔬保鲜贮藏的有效性,而果蔬集装预冷工艺以及包装结构对流态冰预冷果蔬影响的研究甚少。
托盘集装预冷是果蔬采后预冷的高效处理技术方式[12],能有效降低能耗,提高预冷效率。针对流态冰预冷,国外已实现了自动化托盘集装充冰预冷[13],国内相关应用研究较晚,集装充冰还未实现产业化。集装充冰预冷过程中多层箱内流态冰分布的均匀性以及各层包装箱内的冰晶质量会直接影响箱内果蔬的局部温度差异,进而影响果蔬预冷和贮运过程中的品质。本文以多层箱装西兰花为研究对象,设计多层箱集装单元化充填流态冰的工艺,通过CFD模拟分析充冰工艺参数对各层包装箱内冰晶分布和冰晶质量的影响规律。采用响应面分析的方法探究充冰角度、充冰速度、充冰时间三者之间的交互作用,确定最佳充冰工艺参数,并进行实际充冰试验和贮存试验,验证仿真结果的有效性,旨在为果蔬预冷及贮运保鲜应用提供技术基础。
1 物理模型及计算方法
1.1 流态冰预冷包装多层箱充冰工艺
目前市场使用的西兰花保鲜大都依赖人工注碎冰的操作,这一过程费时费力,且碎冰潜热低,坚硬棱角容易损伤产品表面。而流态冰冰晶颗粒微小,直径在20~80 μm,在液体中,具有良好的流动性,因此可以借助泵等机械设备进行快速注冰,无需采用人工注冰[14]。为了更好地利用机械设备快速、便捷和标准化的特点,对西兰花多层箱集装单元进行整体注冰则具有显著优势。
流态冰预冷包装多层箱堆码结构如图1所示。纸箱选用淋膜防水纸箱,上下开有通冰孔,两侧均设有充冰孔和排水孔,整体重叠堆码,确保上下2层纸箱的通冰孔对齐。在注冰过程中,注冰设备的充冰枪头与第4层纸箱的充冰孔对接并实施注冰。流态冰依靠自身的流动性和初始动能,从第4层纸箱开始,通过通冰孔,逐级流动至各层纸箱内,冰晶被西兰花表面捕获,逐渐堆积,同时液体从排水孔流出,完成托盘化集装充冰过程。因此,流态冰在箱内流动的效果很大程度上取决于其初始速度和初始速度方向。若速度和方向不合适,将导致流态冰的堆积或溢出并造成浪费。

图1 多层箱堆码结构三视图
Fig.1 Three views of multi-story boxes structure
1.2 多层箱集装包装物理模型建立
本研究依据标准GB/T 37922—2019《托盘单元化物流系统 通用技术条件》中规定的包装尺寸模数并结合西兰花箱内摆放形式,选择一典型包装纸箱规格(600 mm×400 mm×400 mm)、直径180 mm的西兰花为研究对象。在此基础上,建立西兰花流态冰预冷包装多层箱三维模型(图2)。包装箱采用淋膜防水纸箱,重叠放置在托盘上,托盘集装放置4层包装箱,从下到上分别为第1层、第2层、第3层与第4层,总高度为1 750 mm,低于标准GB/T 37922—2019中规定的2 200 mm。箱内西兰花以2×3规格重叠放置2层。每层箱之间设置4个通冰孔(φ40 mm),分布式排列,左右两侧分别开有充冰孔(100 mm×50 mm)和排水孔(60 mm×20 mm)。

图2 多层箱三维模型
Fig.2 Three-dimensional model of multi-story boxes
1.3 控制方程
考虑模拟分析有效性及运算时间限制,模型构建过程中引入以下假设:流态冰为不可压缩流体;忽略分析过程中环境温湿度对流态冰、西兰花、箱体的物理性质影响;忽略充冰过程中流态冰对西兰花的传热过程。基于物理模型将整体计算域划分为2个子区域:流态冰流体域和西兰花固体域,在充冰过程中,西兰花表面作为界面区域,固体域不参与计算。
流态冰由冰晶颗粒和液体2种不同物质组成,流动遵循质量守恒、动量守恒定律。其中冰晶颗粒非常微小,尺寸基本在20~80 μm,故采用欧拉-欧拉双流体模型[15]。该模型在欧拉体系下,针对每一相都建立连续性方程和动量方程,通过两相之间的相互作用力实现耦合,然后分别求解各相的N-S控制方程。将流态冰分为液体相和颗粒相,液相作为主相,颗粒相进行拟流体化作为次相[16]。
1.3.1 连续性方程
为描述流态冰在空间和时间上的质量守恒,基于质量守恒定律,建立流态冰的连续性方程如公式(1)和公式(2)所示:
(1)
在两相流模型里面,截取的微元控制体质量变化增加了各相之间的质量传递相,因此第n相的连续性方程为[17]:
(2)
式中:ρn,第n相流体的密度,kg/m3;αn,第n相流体的体积分数;![]() 第n相的速度矢量,
第n相的速度矢量,![]() 第w相到第i相的质量输送,
第w相到第i相的质量输送,![]() 第i相到第w相的质量输送,kg;Sq,源项,此处为零。
第i相到第w相的质量输送,kg;Sq,源项,此处为零。
1.3.2 动量方程
为模拟流态冰在压力、密度和流速等因素下的运动,建立流态冰在流动过程中的动量方程如公式(3)公式(4)所示:
(3)
通过牛顿第二定律,推出控制单元体重第n相的动量变化:
![]()
(4)
式中:![]() 体积力项;
体积力项;![]() 表面力项;
表面力项;![]() 第n相的压力应变张量;
第n相的压力应变张量;![]() 相与相之间的相互作用力,
相与相之间的相互作用力,![]() 重力加速度,
重力加速度,![]() 两相间动量交换;
两相间动量交换;![]() 第n相的外部体积力,
第n相的外部体积力,![]() 第n相的升力,
第n相的升力,![]() 第n相的壁面润滑力,
第n相的壁面润滑力,![]() 第n相的虚拟质量力,
第n相的虚拟质量力,![]() 第n相的湍流耗散力,N。
第n相的湍流耗散力,N。
1.4 初始条件及仿真设置
利用ANSYS Fluent进行求解,设置双精度求解器,采用欧拉-欧拉双流体模型,模拟流态冰的液固属性以及流动状态。两相分为水相和冰晶颗粒相,冰晶颗粒直径统一设置为50 μm。动量、湍动能的离散格式为二阶迎风格式,湍流模型选择Realizable k-epsilon模型,压力速度耦合采用SIMPLEC算法,包装箱采用淋膜防水纸箱,通过试验计算测得西兰花(25 ℃)、流态冰(0 ℃)和包装箱(25 ℃)的密度分别为910.0、758.0、220.0 kg/m3,流态冰的动力黏度为0.000 513 kg/(m·K)。
2 模拟分析与实验验证
结合产品包装及前期流态冰预冷试验相关结果,选择一组典型充冰工艺参数为例进行分析,即充冰速度(流量)和充冰角度。充冰速度设置为1、2、3、4 m/s,相对应的进口流量为2.5、5、7.5、10 kg/s。充冰角度以进口速度方向和X轴水平线夹角设置0 °、30 °、60 °,向下为正。流态冰体积分数设置为30%、充冰时间为80 s。
2.1 充冰速度对箱内冰晶均匀性和冰晶质量的影响
在保持充冰时间80 s、充冰角度0 °条件下,分析得到不同充冰速度下箱内冰晶颗粒分布云图如图3所示、每层箱内冰晶质量见表1。可以发现随着充冰速度从1 m/s增大至4 m/s,整个托盘单元的冰晶质量增加了17.34%。然而这种增加并非均匀分布在各层箱内,特别是上层箱体,冰晶质量反而逐渐较少,尤其是第4层箱内,冰晶质量减少了24.49 kg,占比79.05%。增加的冰晶堆积在第2层和第3层,造成堵塞。结果表明,充冰速度会影响各层箱内的流态冰质量,速度过快会导致流态冰的堆积,这与流态冰保鲜渔获物的相关研究结果一致[18],流态冰流动速度会影响产品表面对冰晶颗粒的捕获能力,速度增大时,流态冰在有限空间内易发生堵塞。因此对于最佳的充冰效果,需要选择合适的充冰速度,避免冰晶聚集堵塞通冰孔。
表1 各层箱内冰晶质量
Table 1 Mass of ice slurry in each layer
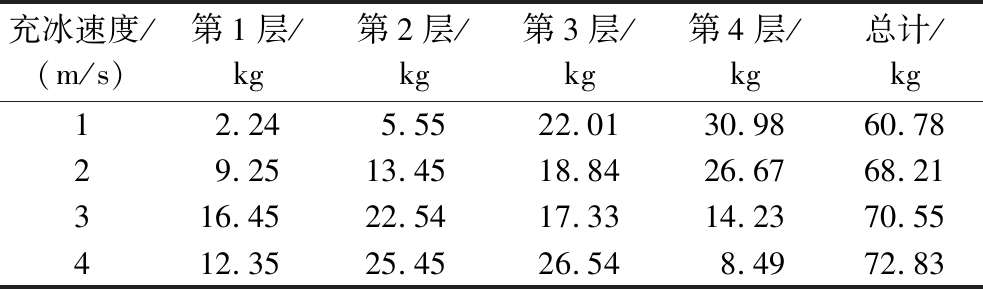
充冰速度/(m/s)第1层/kg第2层/kg第3层/kg第4层/kg总计/kg12.245.5522.0130.9860.7829.2513.4518.8426.6768.21316.4522.5417.3314.2370.55412.3525.4526.548.4972.83
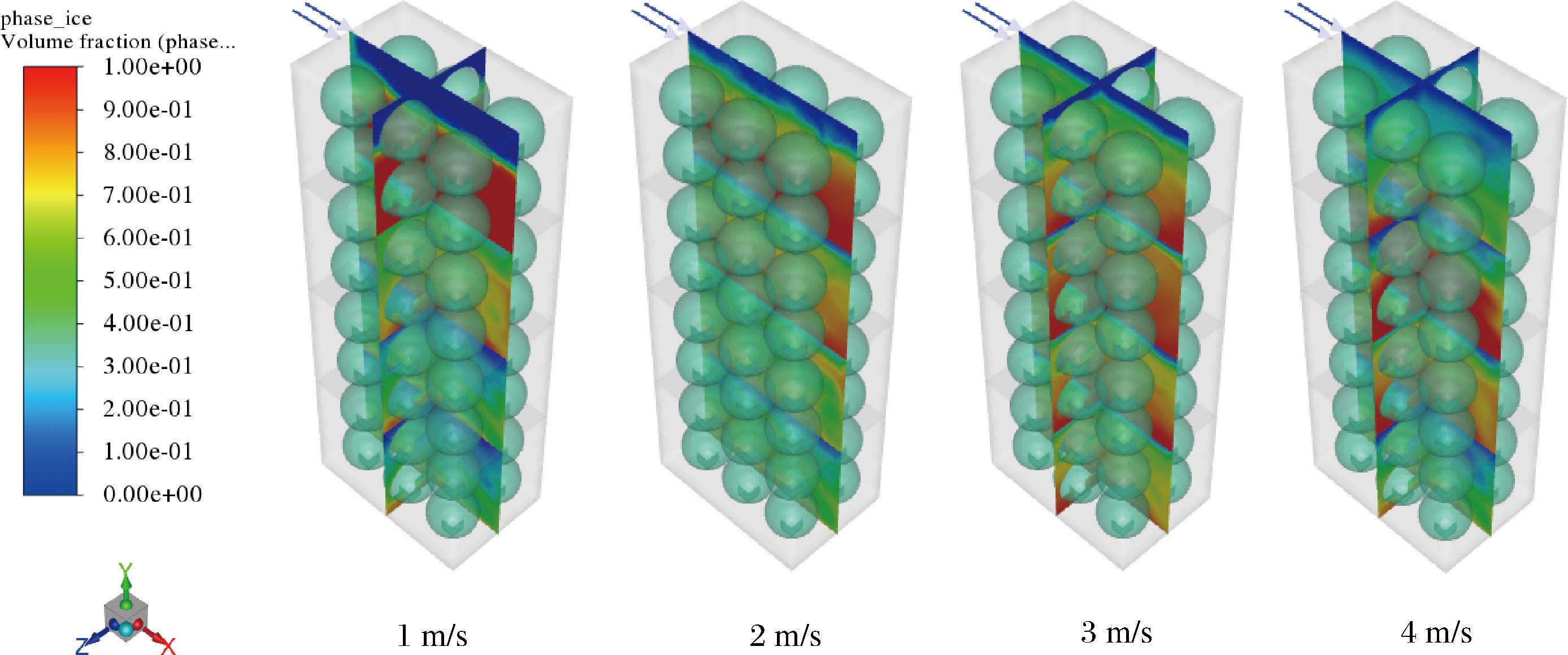
图3 不同充冰速度下箱内冰晶颗粒分布云图
Fig.3 Contour maps of ice crystal particle distribution inside the box at different ice-filling speeds
图4为不同速度下的冰晶颗粒速度矢量图,当速度过小时,流态冰颗粒初始动能较小,流动主要受流态冰自身重力影响,因此遇到西兰花表面时易被捕获,故堆积在第4层箱内;当充冰速度过大时,冰晶颗粒初始动能大,不易被西兰花表面捕获,流态冰迅速流动至中间层并堆积;以上2种情况均会导致流态冰聚集并堵塞通冰孔,不利于流态冰流动。
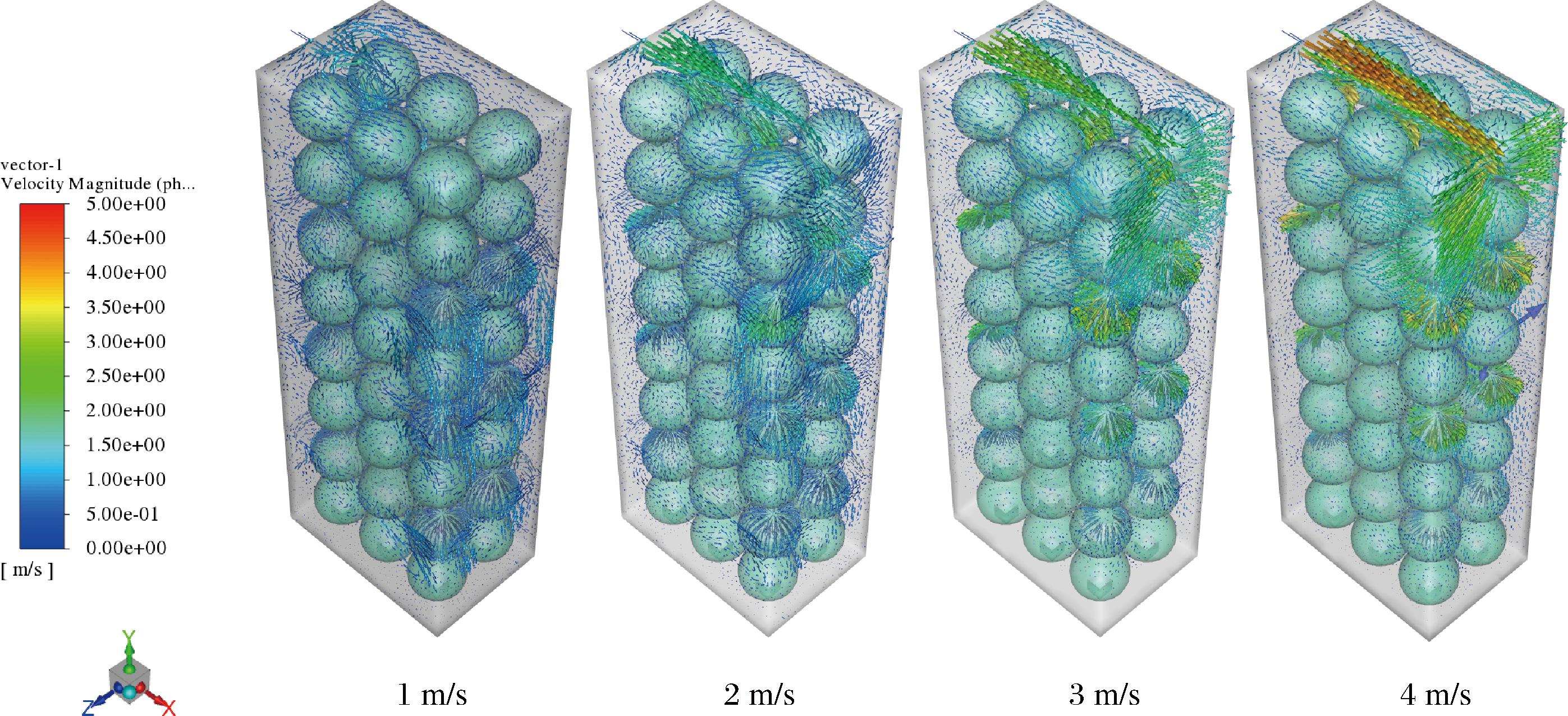
图4 不同充冰速度下箱内冰晶速度矢量图
Fig.4 Velocity vector maps of ice crystals inside the box at different ice-filling speeds
从生产角度分析,箱内冰晶质量越多越好,但从果蔬保鲜及集装贮存角度分析,上层箱体冰晶质量应大于下层箱体。若上层箱内冰晶质量过少,会导致上层箱内西兰花的保鲜时间大大缩短,且过快的速度会造成箱内流态冰分布不均匀。为了更加地准确描述充冰速度对箱内流态冰分布的均匀性,借助压差预冷研究中的预冷均匀度,引入冰晶均匀度来分析[19]。通过箱内西兰花顶部区域的冰晶颗粒占比波动大小来定量分析冰晶均匀度,如公式(5)所示[20]:
(5)
式中:θ为均匀度;N为包装箱内的西兰花数量,![]() 为包装箱内冰晶的平均占比;pi为第i个西兰花顶部区域的冰晶占比。θ越小,表明包装箱内西兰花顶部区域的冰晶分布离散程度越小,分布越均匀,预冷均匀性越好。
为包装箱内冰晶的平均占比;pi为第i个西兰花顶部区域的冰晶占比。θ越小,表明包装箱内西兰花顶部区域的冰晶分布离散程度越小,分布越均匀,预冷均匀性越好。
图5为不同速度下各层箱内冰晶分布均匀度。速度过大或者过小,均会导致个别箱体冰晶分布的不均匀,2 m/s充冰速度下,各层包装箱内冰晶均匀度最小。流态冰的流速增大,流态冰的压降增大[21],流动性变差,因此造成局部冰晶堆积过多,箱内冰晶均匀性变差。并且产品表面的冰颗粒数量增加,会导致流态冰对产品的传热系数增大,进而局部发生冻害现象,不利于保持果蔬品质[22]。
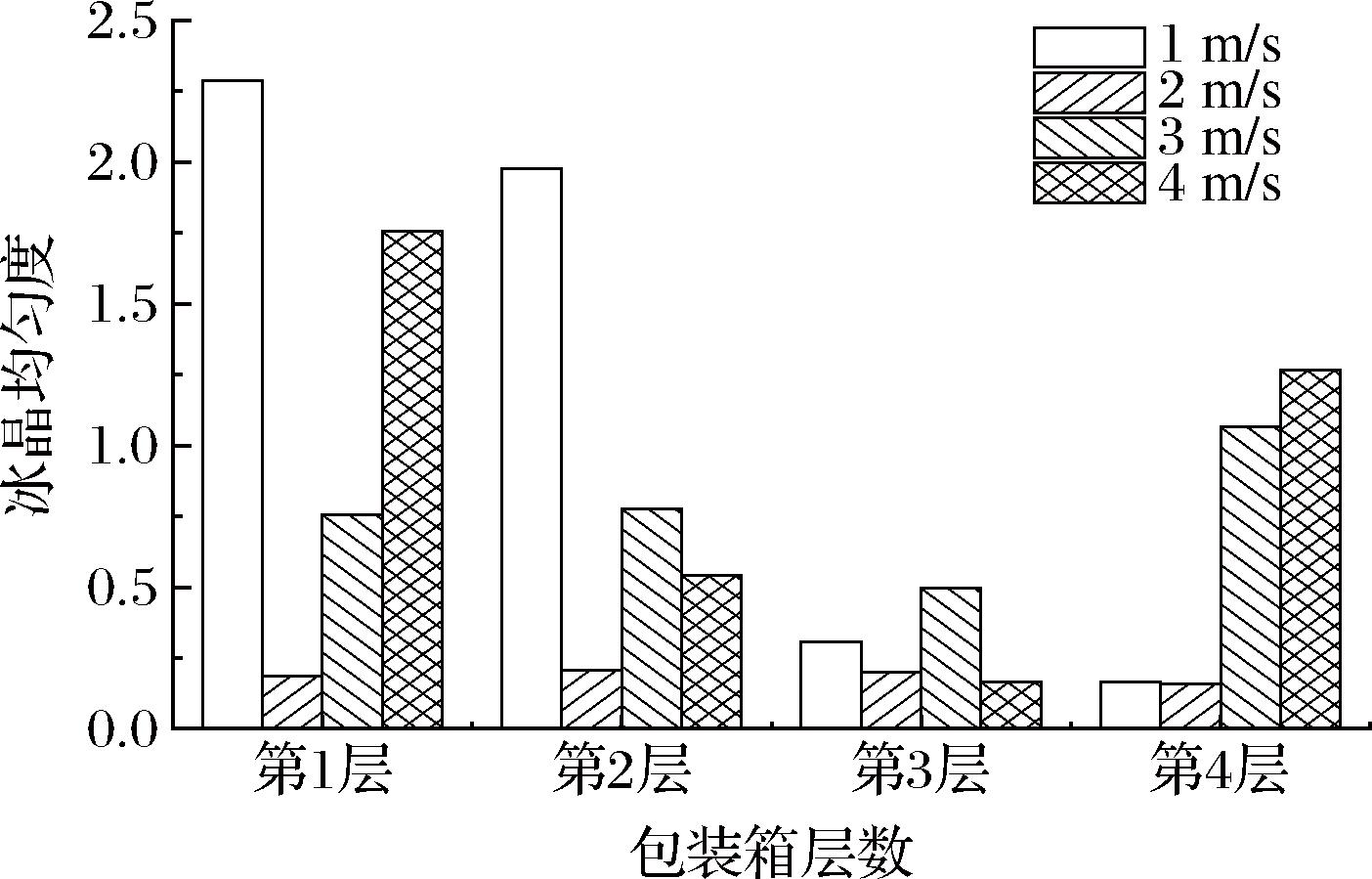
图5 不同充冰速度下的冰晶均匀度
Fig.5 The evenness of ice crystal distribution at different ice-filling speeds
综上所述,充冰速度对箱内冰晶均匀性和冰晶质量都有显著影响,过小或过大的速度均会导致流态冰堆积在某一层内。
2.2 充冰角度对箱内冰晶均匀性和冰晶质量的影响
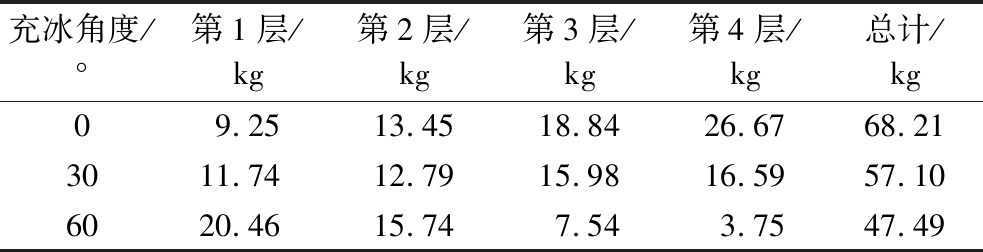
在保持充冰时间80 s、充冰速度2 m/s、进口流量5 kg/s条件下开展分析。图6显示了在不同充冰角度下多层箱内部冰晶的分布情况,表2为不同角度下的箱内冰晶质量。充冰角度控制了流态冰进入箱内的流动方向,充冰角度从0 °增加至60 °时,流态冰向着箱体底部聚集,快速通过通冰孔向下流动,因此第4层箱体内冰晶质量迅速减少,从26.67 kg减少至3.75 kg,减少了85.94 %,流态冰逐渐聚集在第1层箱体内。4层箱总的冰晶质量从68.21 kg减少至47.49 kg,减少了30.38 %,这说明充冰角度极大影响箱内冰晶质量,比充冰速度影响更加显著,且偏斜角度越大,冰晶质量损失越多。
表2 各层箱内冰晶质量
Table 2 Mass of ice slurry in each layer
充冰角度/°第1层/kg第2层/kg第3层/kg第4层/kg总计/kg09.2513.4518.8426.6768.213011.7412.7915.9816.5957.106020.4615.747.543.7547.49

图6 不同充冰角度下箱内冰晶颗粒分布云图
Fig.6 Contour maps of ice crystal particle distribution inside the box at different ice-filling angles
图7为不同充冰角度下箱内冰晶速度矢量图,图8为不同充冰角度下的冰晶均匀度。充冰角度增大会导致冰晶在下层箱体内流动速度增大,尤其是第3层,极易造成流态冰溢出,进而减少箱内的冰晶质量。从冰晶均匀度看,倾斜角度增加导致第4层箱内均匀性偏差快速上升,这是因为冰晶颗粒随着液体流动,液体流向变化会影响冰晶颗粒分布,颗粒在壁面处的剪切应力发生变化。宏观表现就是产品对冰晶颗粒的捕获能力下降,这也导致了第4层箱内流态冰过少,无法覆盖西兰花。

图7 不同充冰角度下箱内冰晶速度矢量图
Fig.7 Velocity vector maps of ice crystals inside the box at different ice-filling angles

图8不同充冰角度下的冰晶均匀度
Fig.8 The evenness of ice crystal distribution at different ice-filling angles
综上所述,充冰角度显著影响箱内流态冰的整体冰晶质量以及分布均匀性。随着充冰角度增大,冰晶质量损失逐渐增加,同时冰晶均匀性逐渐减弱。
2.3 实验验证
实验于北京市农林科学研究院国家蔬菜研究中心进行,采用弗格森制冷机制取体积分数为30%的流态冰,新鲜西兰花采购于北京本地市场,产地为河北。
每组实验共4层纸箱,采用淋膜防水纸箱(600 mm×400 mm×400 mm),装载8 kg西兰花。实验前,所有实验材料放入25 ℃恒温仓库中预处理8 h,并在包装箱内上下两层西兰花的内部,各放置一个温度记录仪。然后进行充冰,随后记录每箱重量,观察箱内冰晶分布状态。图9为实验现场图。设置实验条件为:充冰速度为1、2、3、4 m/s,进口流量为2.5、5、7.5、10 kg/s。充冰角度设置0°、30°、60°。流态冰体积分数设置为30%、充冰时间为80 s。

a-重叠摆放;b-制冰;c-充冰;d-贮存
图9 试验现场图片
Fig.9 Test picture
充冰完成以后,观察箱内冰晶分布状态,图10为在充冰角度0 °、充冰速度2 m/s、进口流量5 kg/s条件下各层箱内冰晶的分布情况。从第4层到第1层,冰晶分布逐级减少,符合仿真结果规律。表3为仿真与实验在各个条件下各层冰晶质量的误差对比,最大误差为12.61%,大部分维持在10%以下。误差的来源主要是试验过程中箱内西兰花大小均匀性及摆放位置。实际过程中,西兰花大小不均匀,在箱内易对流态冰的流动造成阻碍,因此更多的流态冰被留在上层箱内,导致上层箱内多而下层少,这也造成了第1层箱内冰晶质量实验值略低于仿真值。总体上试验结果规律与仿真结果一致,相关参数可作为后续优化设计的基础。
表3 各层箱内冰晶质量
Table 3 Mass of ice slurry in each layer

充冰工艺参数充冰工艺参数值数值类型第1层/kg第2层/kg第3层/kg第4层/kg充冰速度1 m/s2 m/s3 m/s试验2.035.0423.8732.87仿真2.245.5522.0130.98误差9.38%9.19%8.45%6.10%试验8.5711.9820.5229.55仿真9.2513.4518.8426.67误差7.35%10.93%8.92%10.80%试验21.5816.2816.4815.78仿真23.4517.5415.3314.23误差7.98%7.18%7.50%10.89%充冰角度0°30°60°试验8.4712.4419.9229.55仿真9.2513.4518.8426.67误差8.43%7.51%5.73%10.79%试验10.2611.4917.1918.07仿真11.7412.7915.9816.59误差12.61%10.16%7.57%8.92%试验22.7713.988.294.14仿真20.4615.747.543.75误差11.29%11.18%9.95%10.40%

a-第1层;b-第2层;c-第3层;d-第4层
图10 试验结果对比图
Fig.10 Comparison of test results
3 充冰工艺参数优化
3.1 响应面试验因素与水平设置
响应面分析方法是一种综合试验设计方法,可对多个因素进行试验设计,分析各个因素之间的交互协同作用,建立多因素协同作用下,针对试验结果的拟合回归方程,给出各个因素最佳值,提供最优方案[23]。
通过对充冰工艺参数的单因素仿真分析表明充冰角度和充冰速度对冰晶均匀度和冰晶质量的影响规律,同时充冰时间也会直接影响冰晶质量。因此选择3个影响因素进行分析:充冰角度、充冰速度、充冰时间,依次编号A、B、C。根据仿真结果的单因素影响规律,对三者分别设置3个水平,表4为各个因素不同水平值。
表4 响应面试验因素与水平设置
Table 4 Test factors and level setting of response surface

水平因素A(充冰角度)/°B(充冰速度)/(m/s)C(充冰时间)/s-1-3017000280130390
生成响应面试验方案设计表(表5),共17组试验方案,其中5组为中心点重复试验,根据给出的试验方案修改充冰工艺参数并进行数值模拟。经仿真分析得到每组方案所对应的冰晶均匀度和冰晶质量结果见表5,其中冰晶质量为4层包装箱内的冰晶总质量,充冰均匀度为4层箱的平均均匀度。
表5 响应面方案设计及数值模拟结果
Table 5 Response surface test design and numerical simulation results

标准试验号试验号A/°B/(m/s)C/s冰晶均匀度冰晶质量/kg51-302700.80953.9617202800.31568.9933-303801.20258.6674-302900.89559.6410503700.80266.5416602800.23470.3211701901.14162.1448303800.66171.8915902800.10169.33121003900.69270.5591101701.23556.88112-301801.35646.96813302900.16671.98141402800.25867.15131502800.18768.21616302700.17566.13217301801.15462.32
3.2 回归方程建立与检验实验验证
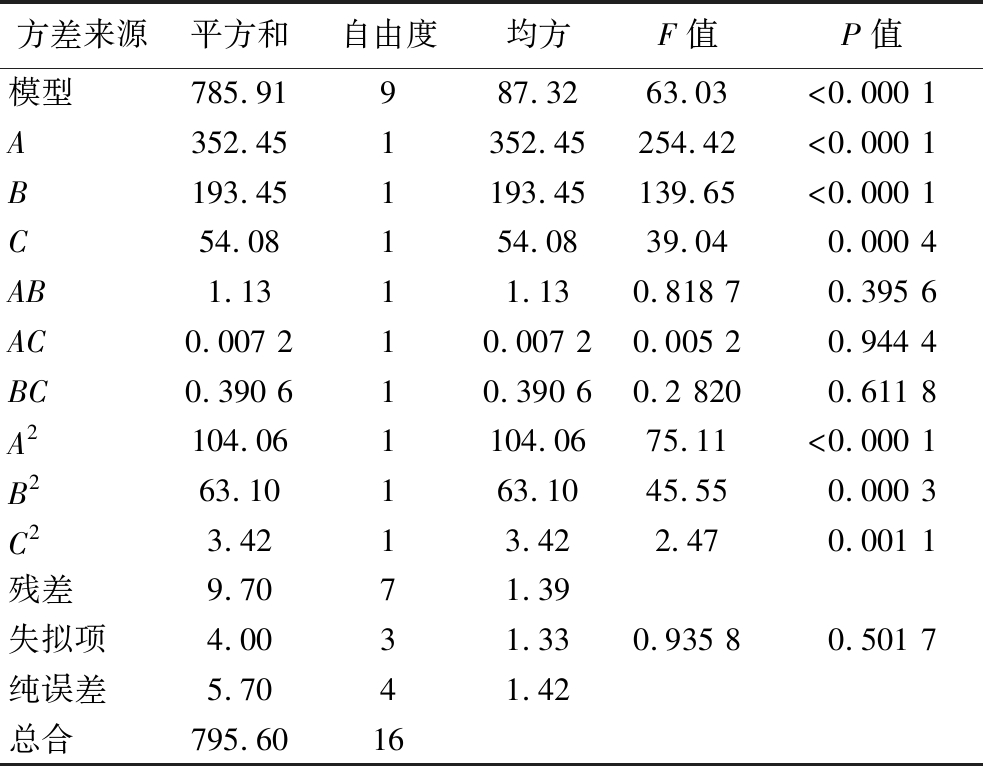
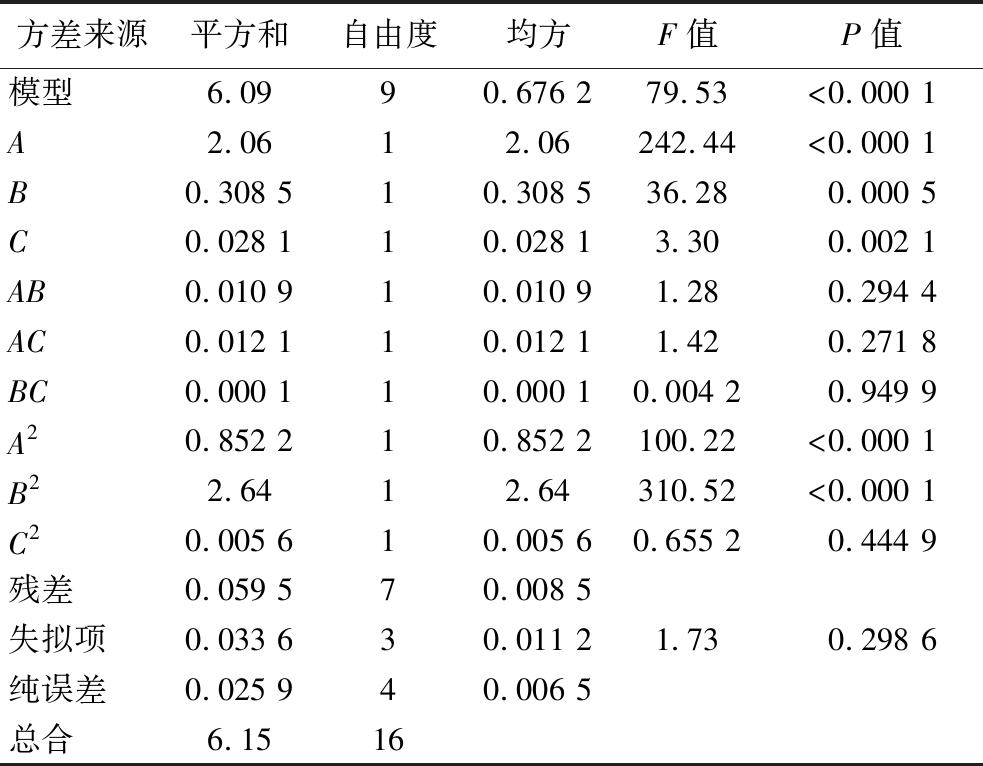
对表5中的结果进行方差分析和显著性检验,拟合模型采用二次多项式(表6、表7)。F值和P值是判断影响因素显著性的指标[24]。在方差结果分析中,A、B因素的P值均小于0.000 1,表示充冰角度、充冰速度对结果的影响具有显著性,符合单因素仿真分析结果,而C因素不具有显著性,说明充冰时间的影响并不显著。根据各个因素的F值评估各因素对冰晶均匀度和冰晶质量的影响程度,排名从高到低为充冰角度>充冰速度>充冰时间。这说明充冰角度对冰晶均匀度和冰晶质量的影响最显著,其次是充冰速度,最后是充冰时间。这些结果有助于进一步确定影响因素的优先级,为工艺参数优化提供了重要参考。
表6 冰晶质量的二次回归方程模型方差分析结果
Table 6 Quadratic regression equation model variance analysis of ice mass
方差来源平方和自由度均方F值P值模型785.91987.3263.03<0.000 1A352.451352.45254.42<0.000 1B193.451193.45139.65<0.000 1C54.08154.0839.040.000 4AB1.1311.130.818 70.395 6AC0.007 210.007 20.005 20.944 4BC0.390 610.390 60.2 8200.611 8A2104.061104.0675.11<0.000 1B263.10163.1045.550.000 3C23.4213.422.470.001 1残差9.7071.39失拟项4.0031.330.935 80.501 7纯误差5.7041.42总合795.6016
表7 冰晶均匀度的二次回归方程模型方差分析结果
Table 7 Quadratic regression equation model variance analysis of ice evenness
方差来源平方和自由度均方F值P值模型6.0990.676 279.53<0.000 1A2.0612.06242.44<0.000 1B0.308 510.308 536.280.000 5C0.028 110.028 13.300.002 1AB0.010 910.010 91.280.294 4AC0.012 110.012 11.420.271 8BC0.000 110.000 10.004 20.949 9A20.852 210.852 2100.22<0.000 1B22.6412.64310.52<0.000 1C20.005 610.005 60.655 20.444 9残差0.059 570.008 5失拟项0.033 630.011 21.730.298 6纯误差0.025 940.006 5总合6.1516
最终获得充冰角度、充冰速度、充冰时间三者协同影响下冰晶均匀度θ和冰晶质量W的回归方程如公式(6)和公式(7)所示:
θ=0.219 0-0.507 6A-0.196 4B-0.059 3C-0.052 3AB+0.055 0AC+0.003 0BC+0.449 9A2+0.791 9B2-0.036 4C2 (R2=0.990 3)
(6)
W=68.80+6.64A+4.92B+2.60C-0.532 5AB+0.042 5AC-0.312 5BC-4.97A2-3.87B2-0.901 2C2(R2=0.987 8)
(7)
式中:θ,冰晶均匀度;W,冰晶质量,kg;A,充冰角度,°;B,充冰速度,m/s;C,充冰时间,s。
3.3 多因素交互作用分析
拟合并验证回归方程后,为探究3个影响因子的交互关系,构建响应面图(图11、图12),分析相关因素之间的交互作用对冰晶均匀度和冰晶质量的影响及其显著性。

a-充冰速度与充冰角度交互作用;b-充冰时间与充冰角度交互作用;c-充冰时间与充冰速度交互作用
图11 不同因素之间的交互作用对冰晶均匀度的影响
Fig.11 Interaction of different factors on the evenness of ice

a-充冰速度与充冰角度交互作用;b-充冰时间与充冰角度交互作用;c-充冰时间与充冰速度交互作用
图12 不同因素之间的交互作用对冰晶质量的影响
Fig.12 Interaction of different factors on the mass of ice
对图11-a进行分析,充冰角度与充冰速度之间存在交互作用,随着两者数值的增加,冰晶均匀度均呈现出先降低后增加的趋势。分析图11-b、图11-c可知,充冰时间与其他2个影响因素之间不存在交互作用,随着充冰时间的延长,冰晶均匀度保持稳定,这是因为当充冰达到一定时间后,会造成流态冰冰晶的堵塞,不利于流态冰流动,因此延长时间并不能显著改善冰晶均匀度。
对图12-a进行分析,充冰角度与充冰速度之间存在交互作用,在单因素分析中,冰晶质量与充冰速度呈正相关,而此处呈现先上升后下降的趋势,说明充冰角度在一定程度上抑制充冰速度对冰晶质量的正向促进作用。分析图12-b、图12-c可知,充冰时间与其他2个影响因素之间存在交互作用,冰晶质量随着充冰时间的延长而增加,但通过等高线分析,曲面较缓,与充冰速度和角度相比,说明影响程度较低,这是因为充冰达到一定时间以后,大多数流态冰会随着水流溢出箱体,同时多余的水流也会带走原本存在的冰晶。
根据响应性分析的结果以及回归方程,针对冰晶均匀度最佳,选择参数为充冰角度13.220°、充冰速度2.218 m/s、充冰时间89.793 s;针对冰晶质量最大,选择参数为充冰角度17.744°、充冰速度2.261 m/s、充冰时间89.356 s;综合考虑2个变量,确定最佳充冰工艺参数为:充冰角度19.165°、充冰速度2.447 m/s、充冰时间89.298 s,预测的冰晶均匀度为0.081,冰晶质量为73.818 kg。
4 结论
以西兰花多层箱预冷包装为研究对象,仿真模拟技术与实验验证相结合,分析多层箱充填流态冰过程中充冰速度和充冰角度对箱内冰晶均匀度与冰晶质量的影响,在此基础上应用响应面分析优化工艺参数。结果表明,充冰角度对冰晶均匀度和冰晶质量影响最大,随着充冰角度的增大,冰晶质量损失逐渐增加,同时冰晶均匀性逐渐减弱。充冰速度的影响是相对的,速度过大或者过小均会导致冰晶均匀性变差。响应面分析结果表明,充冰角度与充冰速度对冰晶均匀性和冰晶质量存在交互影响,其中充冰角度的影响最大。结合响应面分析,综合考虑冰晶均匀度和冰晶质量,确定最佳充冰工艺参数为充冰角度19.165°、充冰速度2.447 m/s、充冰时间89.298 s。本研究仅考虑了充冰工艺参数对冰晶分布的影响,实际包装结构也会影响分布状态。因此,后续研究可进一步探究包装结构对充冰均匀性的影响。
[1] 闫琰, 陈庆敏, 张智, 等.不同物流方式对西兰花品质的影响[J].食品与发酵工业, 2022, 48(12):183-187.YAN Y, CHEN Q M, ZHANG Z, et al.Effects of different logistics methods on the quality of broccoli[J].Food and Fermentation Industries, 2022, 48(12):183-187.
[2] 林酿志, 李传常.相变储能材料及其冷链运输应用[J].储能科学与技术, 2021, 10(3):1040-1050.LIN N Z, LI C C.Phase change materials for energy storage in cold-chain transportation[J].Energy Storage Science and Technology, 2021, 10(3):1040-1050.
[3] 郑恒, 陈大磊, 焦中高. 预冷对果蔬的保鲜作用及其影响因素[J]. 安徽农学通报, 2020, 26(13):137-139;148.ZHENG H, CHEN D L, JIAO Z G. Preservation effect of precooling on fruits and vegetables and its influencing factors[J]. Anhui Agricultural Science Bulletin, 2020, 26(13):137-139; 148.
[4] 贺红霞, 申江, 朱宗升.果蔬预冷技术研究现状与发展趋势[J].食品科技, 2019, 44(2):46-52.HE H X, SHEN J, ZHU Z S.Research status and development trends on precooling technology of fruits and vegetables[J].Food Science and Technology, 2019, 44(2):46-52.
[5] KAUFFELD M, WANG M J, GOLDSTEIN V, et al.Ice slurry applications[J].International Journal of Refrigeration, 2010, 33(8):1491-1505.
[6] 刘瑶, 左进华, 高丽朴, 等.流态冰预冷处理对甜玉米贮藏品质的影响[J].制冷学报, 2020, 41(3):83-90.LIU Y, ZUO J H, GAO L P, et al.Effect of slurry ice precooling treatment on quality of sweet corn[J].Journal of Refrigeration, 2020, 41(3):83-90.
[7] 刘瑶, 左进华, 高丽朴, 等.流态冰预冷处理对西兰花品质及生理的影响[J].现代食品科技, 2019, 35(4):77-86.LIU Y, ZUO J H, GAO L P, et al.Effect of slurry ice precooling treatment on quality of broccoli[J].Modern Food Science and Technology, 2019, 35(4):77-86.
[8] 李翠红, 魏丽娟, 李长亮, 等.流态冰预冷近冰温贮藏对西兰花贮藏品质的影响[J].甘肃农业科技, 2022, 53(9):52-57.LI C H, WEI L Y, LI C L, et al.Effect of fluid-ice precooling at near-freezing point on storage quality of broccoli[J].Gansu Agricultural Science and Technology, 2022, 53(9):52-57.
[9] 时文林, 赵雅琦, 闫志成, 等.不同预冷方式对甜玉米储藏品质的影响[J].食品科学, 2022,43(15):218-226.SHI W L, ZHAO Y Q, YAN Z C, et al.Effects of different precooling methods on storage quality of sweet corn[J].Food Science, 2022,43(15):218-226.
[10] 李淦, 王清, 卢立新, 等.流态冰预冷西兰花温度场数值模拟[J].食品与机械, 2023, 39(7):125-130.LI G, WANG QI, LU L X, et al.Numerical simulation study on temperature field of ice slurry pre-cooled broccoli[J].Food &Machinery, 2023, 39(7):125-130.
[11] 孟维岩, 尹忠俊, 郑秋云, 等.低含冰率冰浆预冷甜玉米温度场的数值模拟研究[J].江苏农业科学, 2019, 47(6):159-162.MENG W Y, YI Z J, ZHENG Q Y, et al.Numerical simulation of temperature field of precooled sweet corn with low ice content[J].Jiangsu Agricultural Sciences, 2019, 47(6):159-162.
[12] 陈秀勤,卢立新.集合包装水果的差压预冷研究进展[J].包装工程, 2014, 35(1):141-147.CHEN X Q, LU L X.Research advances of foced-air precooling for multi-packed fruits[J].Package Engineering, 2014, 35(1):141-147.
[13] KUMANO H, HIRATA T, HAGIWARA Y, et al. Effects of storage on flow and heat transfer characteristics of ice slurry[J]. International Journal of Refrigeration, 2012, 35(1):122-129.
[14] 贾世亮, 张越, 刘关成, 等.流态冰预冷技术及其在冷鲜食品中的应用研究进展[J].食品与发酵工业, 2014, 35(2):176-181.JIA S L, ZHANG Y, LIU G C, et al.Research progress on slurry ice precooling technology and its application in chilled food processing[J].Food &Fermentation Industries, 2014, 35(2):176-181.
[15] ONOKOKO C L, GALANIS N, PONCET S, et al.Heat transfer of ice slurry flows in a horizontal pipe:A numerical study[J].International Journal of Thermal Sciences, 2019, 142:54-67.
[16] 布关印, 陈海文, 徐立, 等.管内冰浆在振动工况下的流动及传热特性[J].哈尔滨工程大学学报, 2021, 42(9):1280-1286.BU G Y, CHEN H W, XU L, et al.Flow and heat transfer characteristics of ice crystals in polar vessel pipelines under vibration conditions[J].Journal of Harbin Engineering University, 2021, 42(9):1280-1286.
[17] JOHN D, ANDERSON. Computational Fluid Dynamics: The Basics with Applications[M]. New York: McGraw-Hill, 1995: 40-41.
[18] 赵新颖,黄温赟,黄文超,等.渔获物冰浆保鲜流动传热分析[J].渔业现代化, 2020, 47(4):74-82.ZHAO X Y, HUANG W B, HUANG W C, et al.Study on flow and heat transfer in fish freshness retaining using ice slurry[J].Fishery Modernization, 2020, 47(4):74-82.
[19] 陈秀勤, 卢立新, 王军.包装箱内层装果品差压预冷温度场的数值模拟与验证[J].农业工程学报, 2014, 30(12):249-257.CHEN X Q, LU L X, WANG J.Numerical simulation and experimental verification of forced-air precooling temperature field inside fruit packaging box with multiple-layer grids [J].Transactions of the Chinese Society of Agricultural Engineering, 2014, 30(12):249-257.
[20] ZHAO C J, HAN J W, YANG X T, et al.A review of computational fluid dynamics for forced-air cooling process[J].Applied Energy, 2016, 168(1):314-331.
[21] MATSUMOTO K, KUBOTA H, UMEHARA Y, et al. Investigation on cohesive force of ice particles in ice slurry for long-term ice storage[J]. International Journal of Refrigeration, 2018, 90:156-162.
[22] 邢震. 保鲜剂、降温方式结合冰温对大久保桃采后品质影响的研究[D]. 石河子: 石河子大学, 2010.XING Z. Effects of preservatives, cooling methods and ice temperature on postharvest quality of Okubo peach[D]. Shihezi: Shihezi University, 2010.
[23] 王晓静, 王锡尧. 基于响应面法和CFD的平行板反应器流场优化设计[J]. 化工机械, 2020, 47(5):617-625.WANG X J, WANG X Y. Optimal design of flow field of parallel-plate reactor based on response surface methodology and CFD[J]. Chemical Engineering &Machinery, 2020, 47(5):617-625.
[24] 何雪颖, 王平智, 李明, 等. 基于响应面法的表冷器-风机集放热系统参数优化[J]. 农业机械学报, 2020, 51(12):315-323.HE X Y, WANG P Z, LI M, et al. Parameters optimization of greenhouse air-cooled condenser heat collection and release system by response surface method[J]. Transactions of the Chinese Society for Agricultural Machinery, 2020, 51(12):315-323.