传统酱卤肉制品因其独特风味深受我国消费者的喜爱。目前传统热力杀菌工艺加热时间长、温度高会使产品出现汁液渗出、肉质软烂的现象,造成品质下降。微波加热技术与传统加热技术相比具有方便和高效的优势,广泛应用于食品加工等领域[1]。但由于电磁波在微波腔内壁上反射形成的驻波与入射波产生的电场叠加造成电场强度分布不同,使微波加热具有明显不均匀性[2]。此外样品的形状、尺寸和位置,也可能会加剧微波加热的不均匀性,造成产品加热不充分或者焦糊等问题,降低食品加工的安全性,影响食品的质量[3],因此有必要提升微波加热的均匀性。目前主要有2个改进途径:一是提高微波腔内电磁场的均匀性,二是提高微波能量吸收的均匀性[4]。常规的微波加热优化需要通过实验测定,费时费力,随着仿真模拟技术的成熟,数学模拟技术使条件优化变得更为简单、方便,现已广泛用于微波食品的开发、微波工业装备的设计等领域[5]。
通过模拟仿真不同运动方式,以改变加热过程中样品的位置是优化均匀性的重要方法。
等[6]通过数值模拟,提出直线和旋转相结合的运动方式改善微波均匀性,结果表明直线和旋转相结合的运动方式冷点处升温更快,证明物料随机运动可以有效提高微波干燥均匀性。YE等[7]提出矩形多模腔中旋转提升运动,用仿真方法分析了旋转对微波加工过程中温度均匀性的影响。本项目以传统卤肉制品为研究对象,采用旋转叠加翻转的方式提升微波加热的均匀性。借助COMSOL仿真软件对旋转叠加翻转的微波加热过程进行多物理场仿真模拟,分析卤肉制品内部的电磁场分布情况与微波能的吸收效果,揭示卤肉制品内部的电磁场与温度的变化规律,为微波加热技术在酱卤肉类产品中的生产应用提供理论依据。
1 材料与方法
1.1 材料与试剂
鸡腿、香辛料,安徽省滁州市凤阳县天润发超市;浓缩乳清蛋白粉(食品级),南京高溯生物科技有限公司;D-核糖、L-赖氨酸(食品级),河北华阳生物科技有限公司;无水氯化钙(化学纯),上海麦克林生化科技有限公司。
1.2 仪器与设备
Key SIGHT E5071C矢量网络分析仪,是德科技(中国)有限公司;RWBX-08S型微波杀菌机,南京苏恩瑞干燥设备有限公司;DNP-90521A型恒温培养箱、DK-S24型水浴锅,上海三发科学仪器有限公司;HM-TPH21Pro型手持红外测温仪,杭州微影软件有限公司;WT3003型电子天平,精度0.01 g,杭州万特衡器有限公司。
1.3 实验方法
1.3.1 模拟鸡腿的制作
1.3.1.1 介电特性测量
本研究使用上海海洋大学开发的检测系统测量卤鸡腿的介电常数[8]:测试前先开机预热30 min,将测试探头底面紧贴卤鸡肉表面,确保不与外部空气接触造成实验误差。卤鸡肉温度由恒温油浴锅控制,测量卤鸡肉温度为20～100 ℃,每间隔5 ℃记录其介电常数,环境温度为25 ℃。对每个试样进行3次测定,取其平均值为实验结果。
1.3.1.2 模拟鸡腿制作
为避免鸡腿形状差异而造成的实验误差,选择使用模拟鸡腿代替真实鸡腿。模拟鸡腿的制作以胡蕾琪等[8]介绍的模拟食品配方为基础,通过调整无水氯化钙、L-赖氨酸、D-核糖等含量,使模拟鸡腿与真实卤鸡肉的介电性能保持一致,最后将模拟鸡腿的配料与水混合后灌入自制的鸡腿模具中,定型后脱模,最后制得形状一致的模拟鸡腿。
1.4 微波加热数值模型的构建
1.4.1 仿真方法
本仿真几何模型以RWBX-08S型微波杀菌机为原型,如图1所示。该模型包括加热腔体、矩形波导、玻璃转盘以及待加热鸡腿,模型的输出功率为500 W,微波频率为2.45 GHz,波源模式为TE10。卤鸡腿位于转盘的中心位置,会跟随转盘进行圆周旋转,且每隔28 s上下翻转一次。卤鸡腿的初始温度为298.15 K。
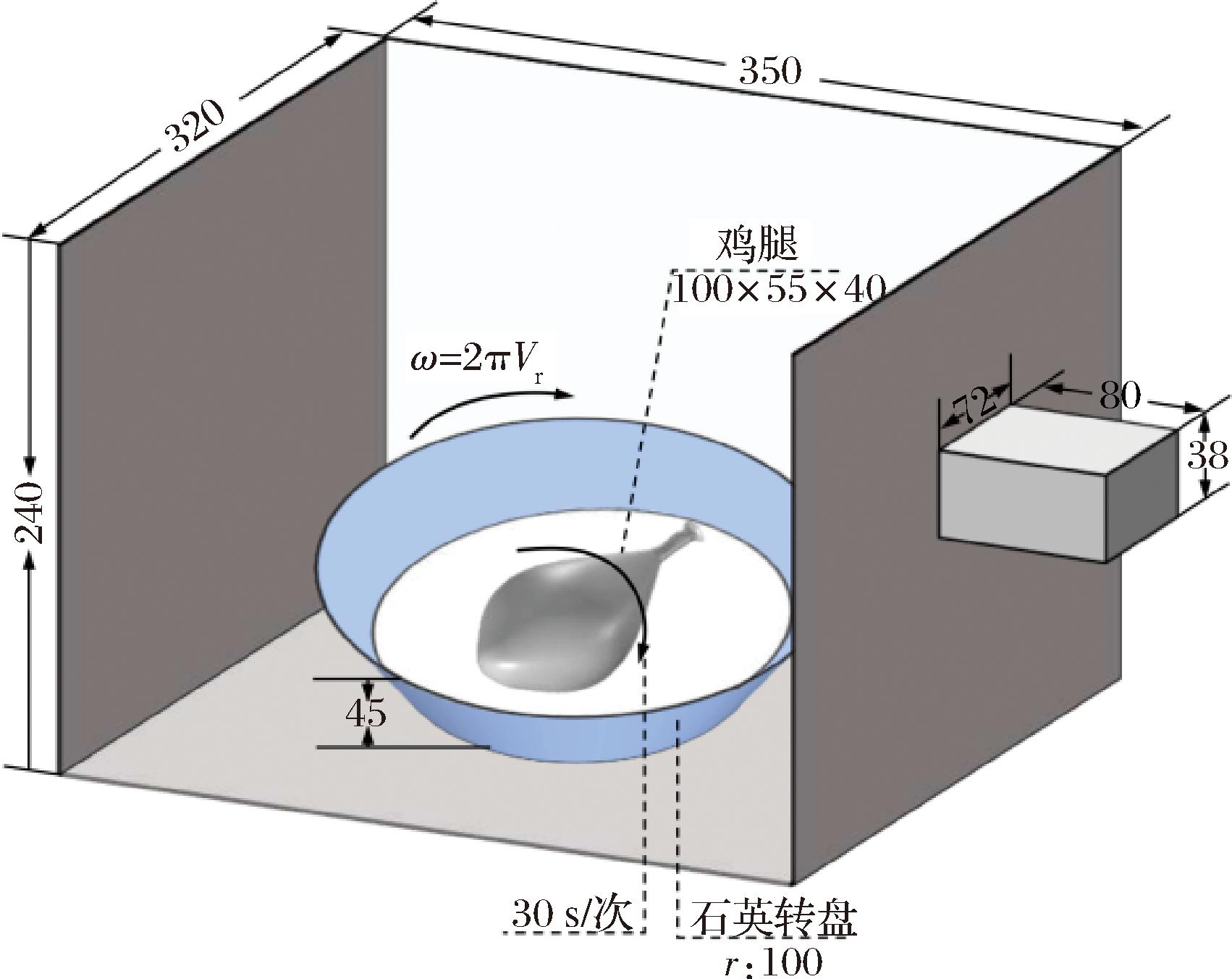
图1 微波炉加热卤鸡腿几何模型图
Fig.1 Geometric diagram of microwave heating marinated chicken leg
1.4.2 控制方程
本研究通过COMSOL multiphsics仿真软件建立微波加热模型,研究卤鸡腿在旋转叠加翻转运动下温度变化及微波电场情况。微波炉腔体内部的电磁能量分布由麦克斯韦方程决定[9],如公式(1)所示:
(1)
式中:μr,相对渗透率;
电场强度,V/m;k02,波数;εr,相对介电特性;σ,电导率,S/m;ω,角频率,rad/s。
当电磁波穿过仿真对象的介电损耗介质时,其强度会减弱,部分电磁能被转换成仿真对象内部的热能,电磁能转换成热能的耗散功率与损耗因子和电场强度的平方成正比,计算如公式(2)所示[10]:
(2)
式中:Pv,耗散功率,W/m2,f,频率,Hz;ε0,真空介电特性,8.854×10-12 F/m;ε″,损耗因子。
耗散功率由傅里叶方程决定[11],如公式(3)所示:
(3)
式中:ρ,密度,kg/m3;Cp,恒压比热容,kJ/(kg·℃);T,仿真时间t时刻的温度;k,导热系数,W/(m·℃)。
在开始工作之前,卤鸡腿的初始温度为25 ℃,卤鸡腿表面与空气发生热量交换,其表面的热量边界条件表示为公式(4)[12]:
(4)
式中:Tn,环境温度,h,表面对流换热传递系数,W/(m2·℃)。
1.4.3 材料参数
微波加热数值分析中,需要输入介电常数、恒压热容、密度以及导热系数等材料参数。表1为模型中各种不同材料的性能参数。
表1 材料性能参数
Table 1 Material performance parameters
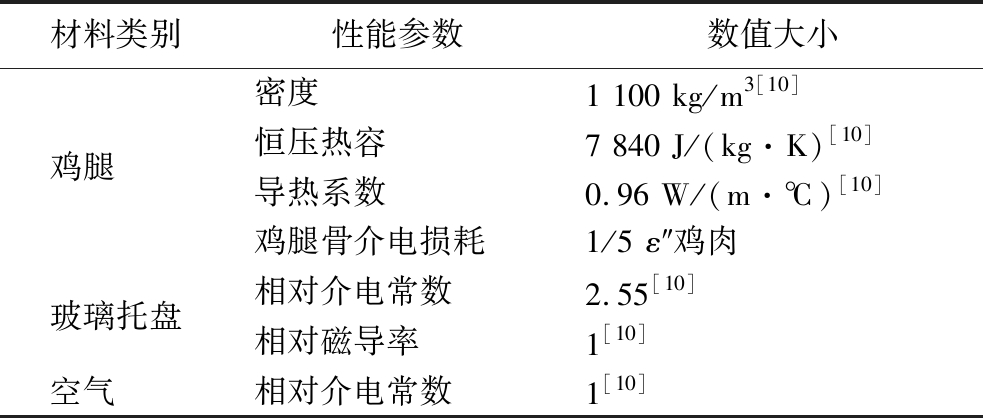
材料类别性能参数数值大小密度1 100 kg/m3[10]鸡腿 恒压热容7 840 J/(kg·K)[10]导热系数0.96 W/(m·℃)[10]鸡腿骨介电损耗1/5 ε″鸡肉玻璃托盘相对介电常数2.55[10]相对磁导率1[10]空气 相对介电常数1[10]
1.4.4 模型假设与边界条件
金属波导和微波炉腔壁可看作完美的电导体,即能完全反射电磁波,适用于边界条件公式(5):
E切向=0
(5)
在模拟加热的过程中,为简化计算过程,做出如下模型假设:
a)模型中鸡肉与骨头视为相同材质,不考虑骨头和鸡肉之间的电磁学特性差异;
b)以空气作为换热媒介,其温度保持恒定,设定为起始温度;
c)除卤鸡腿外,转盘等配件不存在热量传递。
在端口边界条件处,矩形端口在传播方向上没有电场分量,TE10模式是通过矩形波导的唯一传播模式,端口条件需要传播常数β,在频率V下,该常数由公式(6)给出[13]:
(6)
在该仿真模型中,端口频率为2.45 GHz,微波功率为500 W。同时利用波动方程接口给加热对象赋予边界条件,电位移为介电损耗。
1.4.5 网格划分
为获得合理的数值分析模拟结果,模型中所有区域的网格均采用自由四面体网格进行划分,在保证运算时间以及良好的温度仿真结果的前提下,卤鸡腿最合适的网格尺寸该频率和自由空间波长以及介电常数存在的关系如公式(7)所示[14],将波长的1/6定为最大网格单元尺寸,鸡肉网格数为140 858个,鸡肉体积为12.1 cm3。其中全部求解域的单元数为254 992个,平均单元质量为0.653 3。网格划分结果如图2所示。
(7)
图2 微波加热仿真模型的网格划分图
Fig.2 Meshing diagram of simulation model
1.4.6 模拟方法
本研究基于有限元方法,采用移动网格对卤鸡腿运行方式、运动轨迹及运动范围进行剖分界定,其计算步骤如图3所示。通过建立动网格接口,实现网格的自适应更新,解决网格变形问题。在每一次计算结束后,对网格质量进行检测,如果质量低于最小临界,就会进行下一次的划分,如果没有达到最小阈值,就会继续使用原网格进行模拟。在模拟的微波加热条件下,该系统的控制旋转的运动公式如公式(8)所示:
(8)
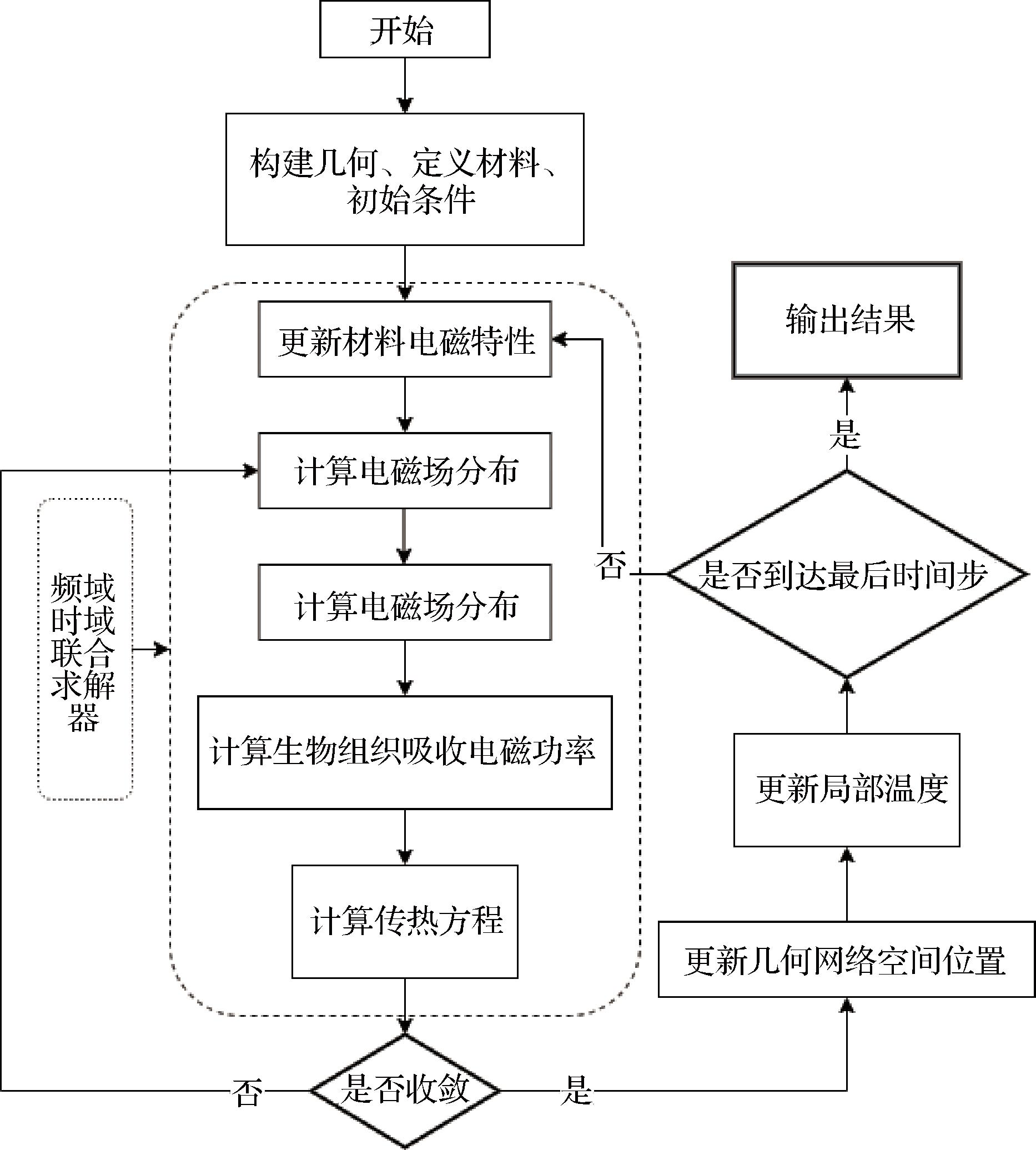
图3 仿真模型计算步骤
Fig.3 Simulation model calculation steps
因为卤鸡腿每隔一段时间需要进行翻转,利用如图4所示的翻转函数来实现Z轴方向的翻转。
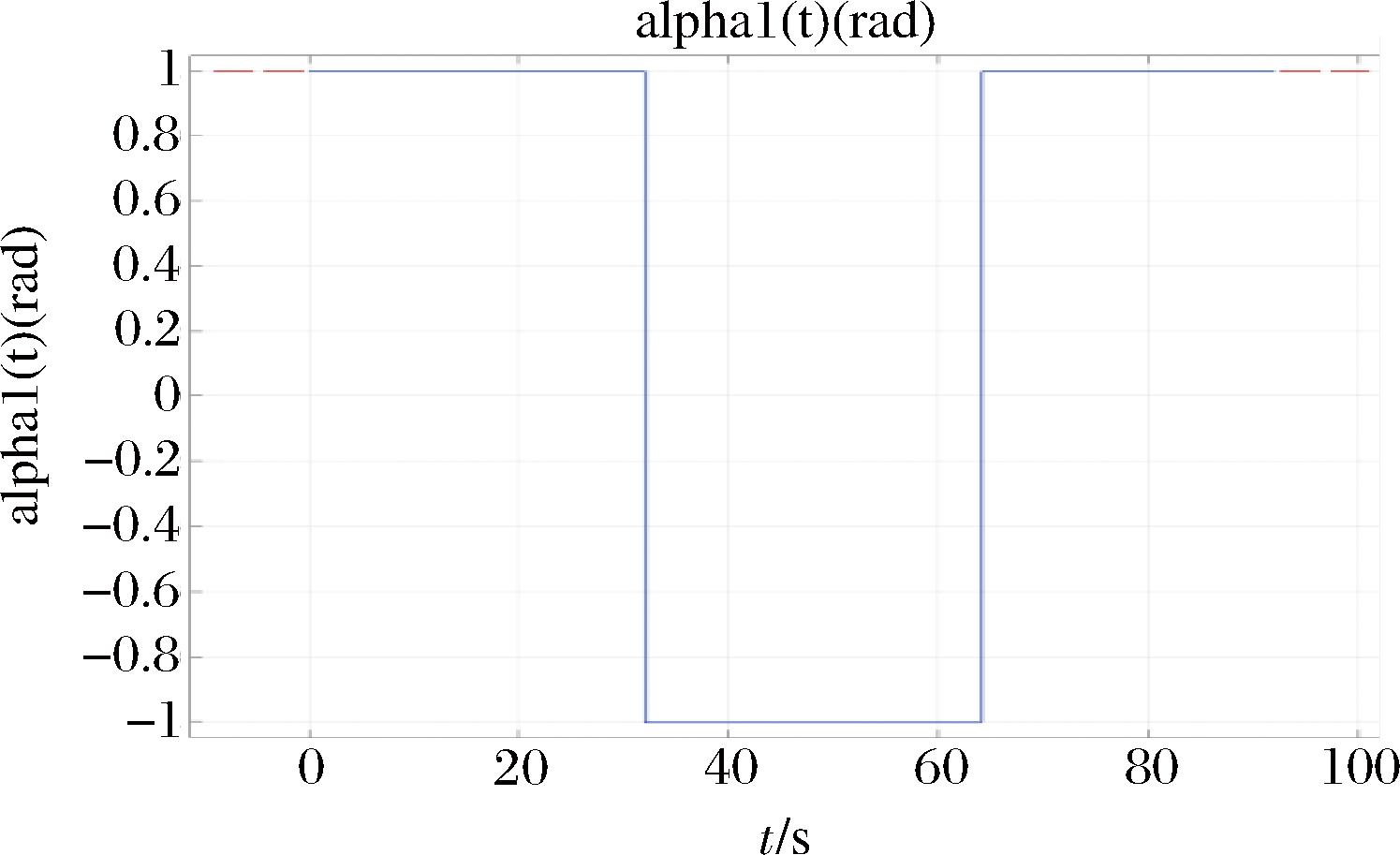
图4 Z轴方向翻转函数
Fig.4 Z-axis direction flip function
1.5 模拟结果的验证
1.5.1 模拟鸡腿温度的测定
为验证仿真模型的精度,通过测量模拟鸡腿与仿真模型的特征点瞬态温度,并计算温度的均方根误差[15](root mean square error, RMSE, %)如公式(9)所示,来验证模型的精确度。
如图5所示将制作的模拟鸡腿放置在转盘中心,设置功率为500 W,持续加热至30 s,关闭机器将鸡腿迅速翻转一次,再重新启动机器直至加热结束。为减少因暂停而造成的热量损耗,实际计时中功率上升的时间不计入加热时间。加热过程中每隔5 s取出并更换实验样品,使用红外热像仪测量温度分布。每组实验重复3次,实验结果用平均值±标准偏差表示。
(9)
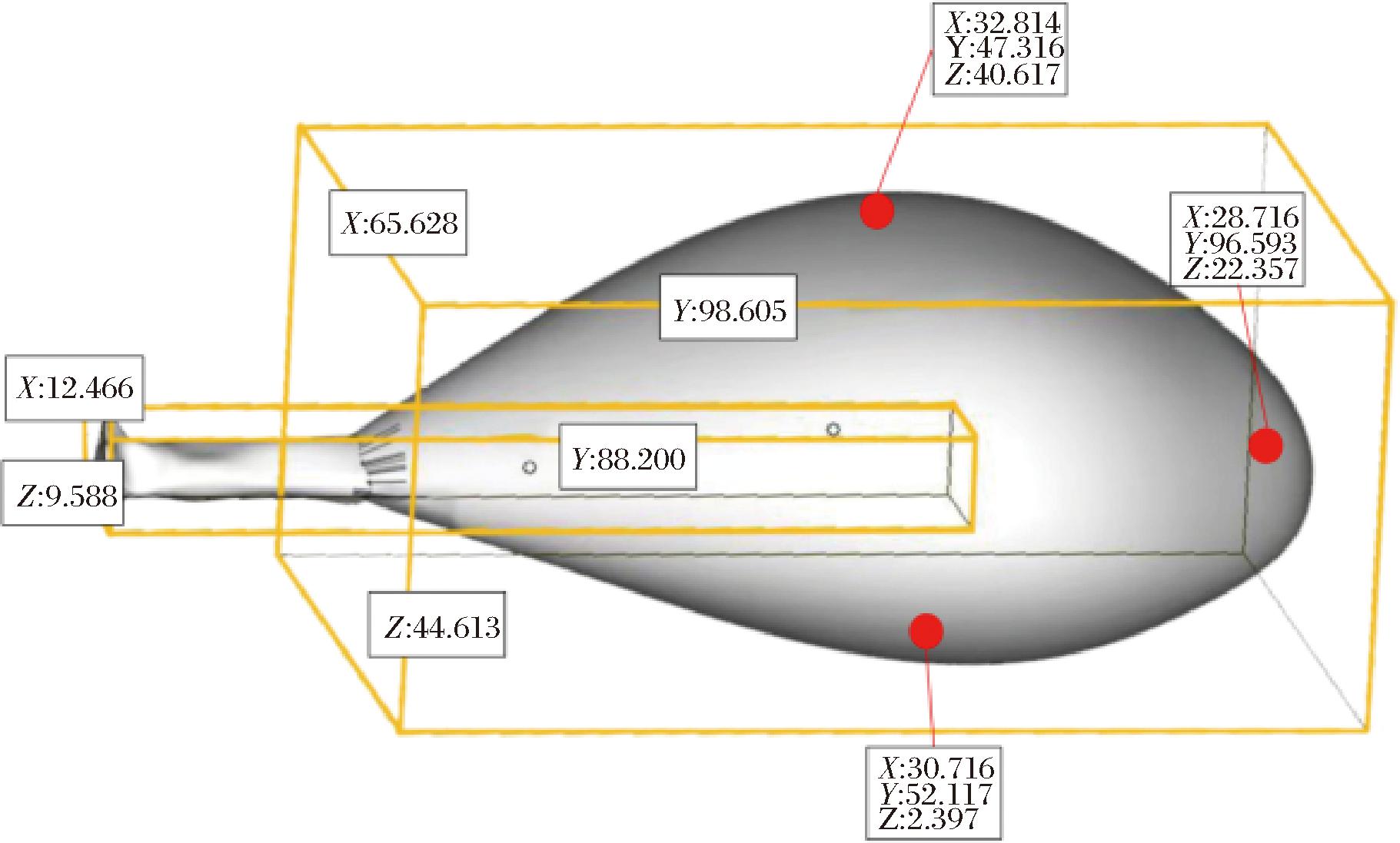
图5 瞬态测温特征点分布示意图
Fig.5 Distribution of transient temperature measurement feature points
式中:Ts,点位仿真温度,℃;Te,测量点位温度,℃;i,测量数;n,数据点总数。
1.6 数据分析
1.6.1 均匀性评价指标
为了定量评价干燥的电场和温度的均匀性,使用MATLAB软件(R2019a)对图像进行处理。引入均匀性系数COVE、COVT和COVδ评价均匀性程度,均匀性系数越低,表明分布的均匀性越高[16]。COVE、COVT和COVδ的计算如公式(10)～公式(12)所示:
(10)
(11)
(12)
1.6.2 热区分布值
参考高明[17]的方法:使用MATLAB软件(R2019a)对图像进行处理,采用K-means聚类法计算温度聚焦区域,并对物料区域分成等面积的i个区域(取i=10),分别计算聚焦区在i个区域中的面积与聚焦区面积之比,得到聚焦区分布曲线,进而确定热区分布值(hot zone distribution, HTD)。其中,HTD越大代表热区集中,温度均匀性越差。
2 结果与分析
2.1 模拟鸡腿的仿制结果与分析
在频率为2 450 MHz,温度20～100 ℃,经实验确定模拟鸡腿的配方如下:无水CaCl2为0.2%、乳清蛋白粉含量为0.5%,D-核糖与L-赖氨酸含量分别为1.5%。2 450 MHz下20～100 ℃内卤鸡腿与模拟食品介电特性的对比如图6所示,模拟鸡腿和真实卤鸡腿的介电特性匹配度较高,可作为用于卤鸡腿的微波实验。
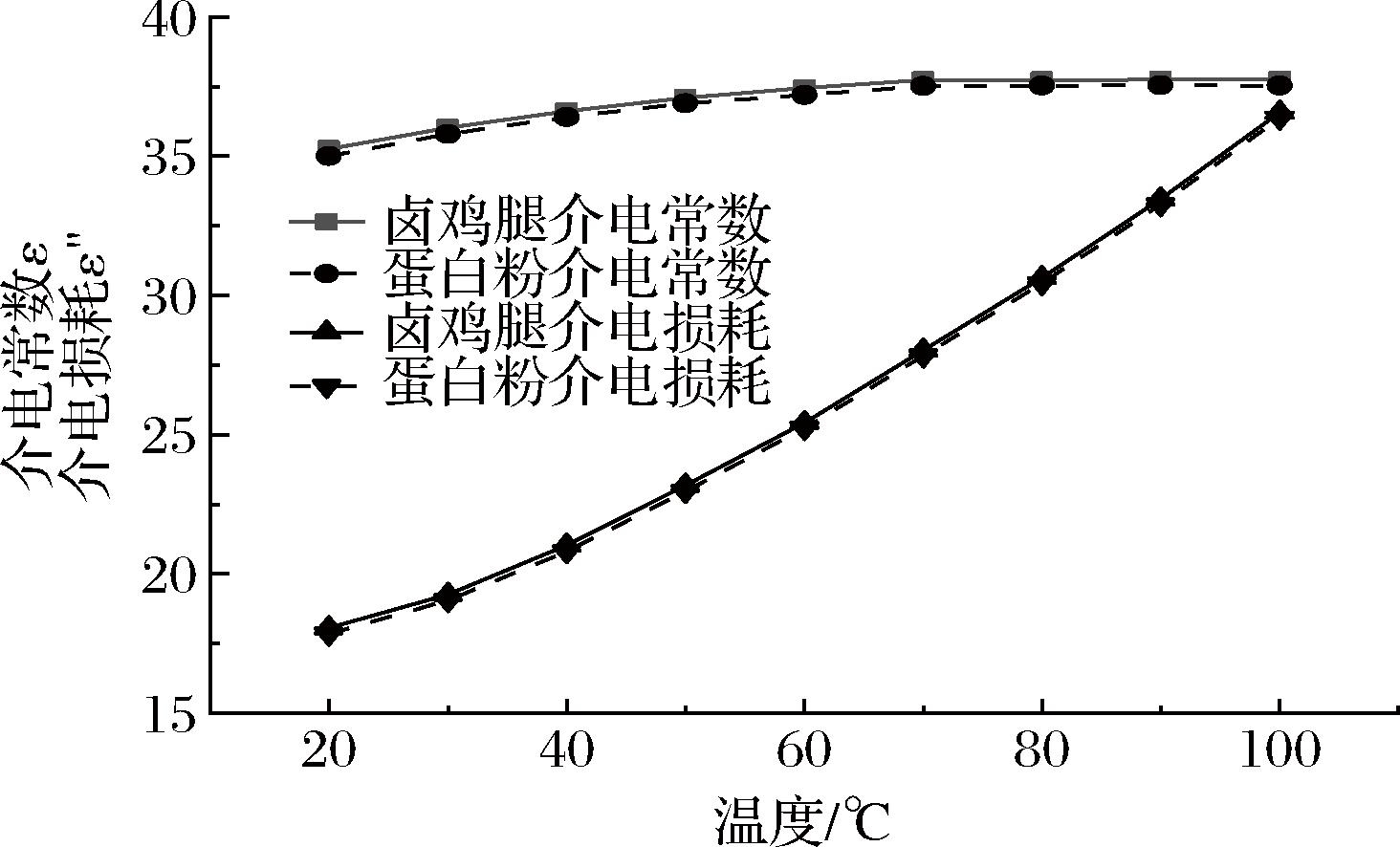
图6 卤鸡腿与乳清蛋白模拟食品介电特性拟合
Fig.6 Comparison of dielectric properties of whey protein model food and stewed chicken leg
2.2 温度场拟合结果与分析
2.2.1 样品特征点位温度对比
从图7可以看出,3个特征点的拟合温度与实测温度的数值大小和变化趋势基本一致,两者的RMSE分别为4.12%、4.97%、3.79%,表明所建立的微波加热卤鸡腿温度场拟合模型准确有效。但模拟温度高于实测温度,可能是由于实验操作时暂停微波设备的滞后带来的影响。
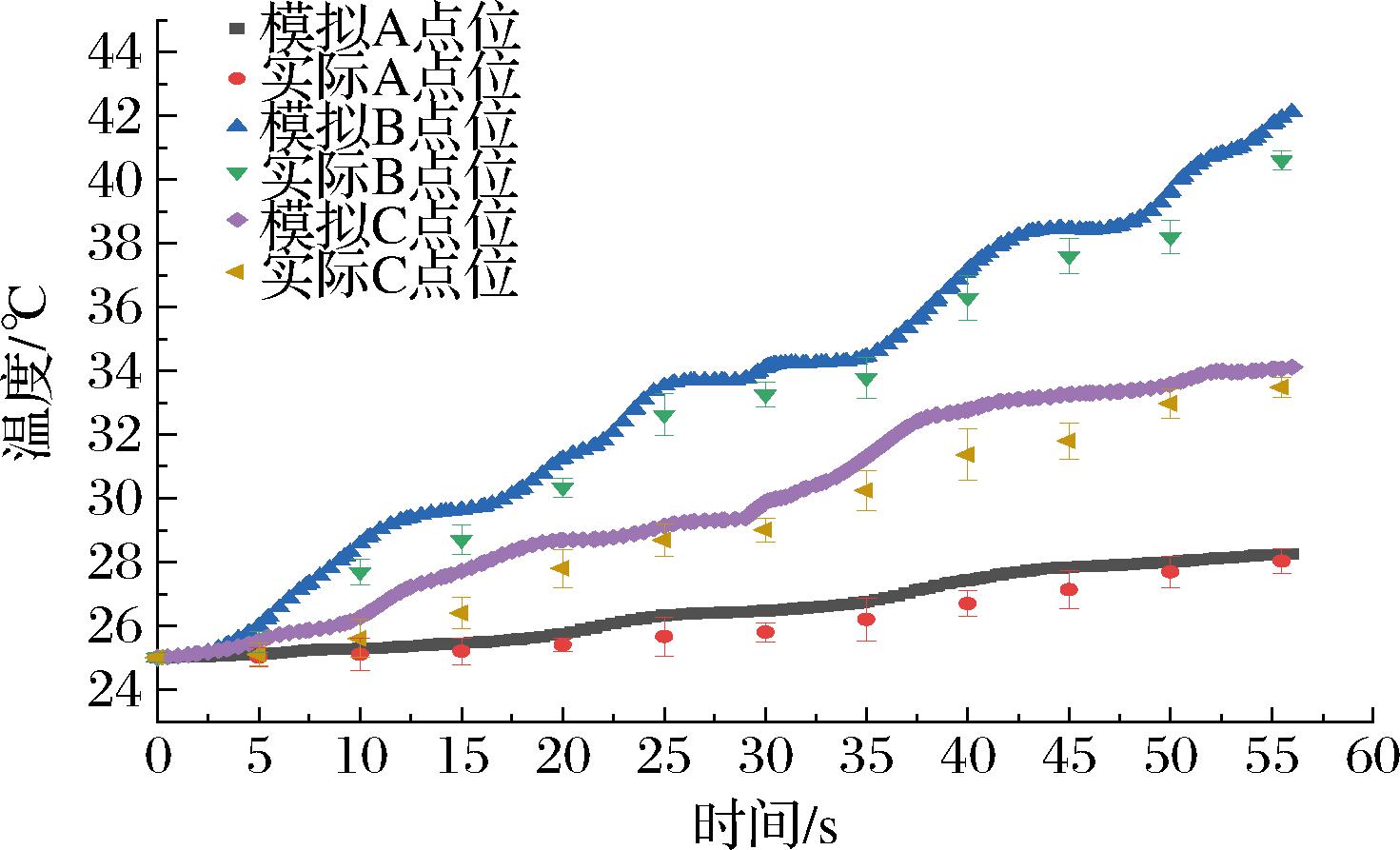
图7 实际样品与仿真样品的特征点温度曲线
Fig.7 Temperature curves of characteristic points between actual and simulated samples
2.2.2 样品表面温度分布与均匀性对比
卤鸡肉在微波加热过程中各阶段对应的温度分布如图8所示。翻转前(7～28 s),卤鸡肉边角温度上升较快,热点逐渐在边角位置形成,中心部位温度上升较慢,导致边角与中心温度差逐渐扩大;翻转后(28～53 s),卤鸡腿上层变为下层,温度快速上升,但卤鸡腿中心温度仍然上升较慢。根据卤鸡腿微波加热过程中温度变化,其均匀性指标如图9所示。卤鸡腿的温度均匀系数随着加热的进行而逐步增大,特别是在前40 s增长快速,达到0.37之后,增长趋势基本停滞。热区分布值在前13 s快速增大至0.45,之后又迅速下降至0.2左右,并趋于稳定。翻转对温度均匀系数增长起到了明显的抑制作用,说明翻转有助于卤鸡腿温度的均匀。
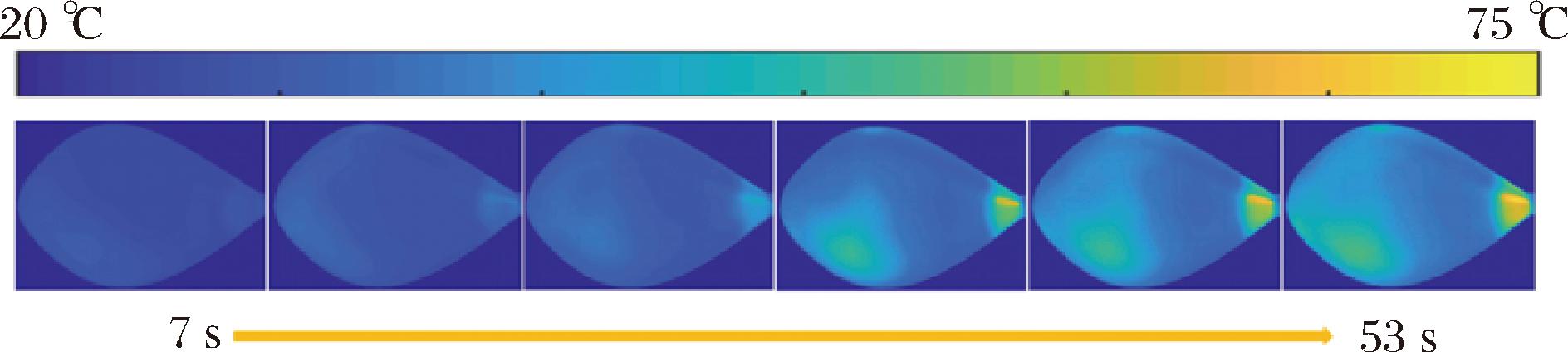
图8 样品表面温度随微波加热变化的热力分布图
Fig.8 Thermal distribution of surface temperature of the sample as a function of microwave heating
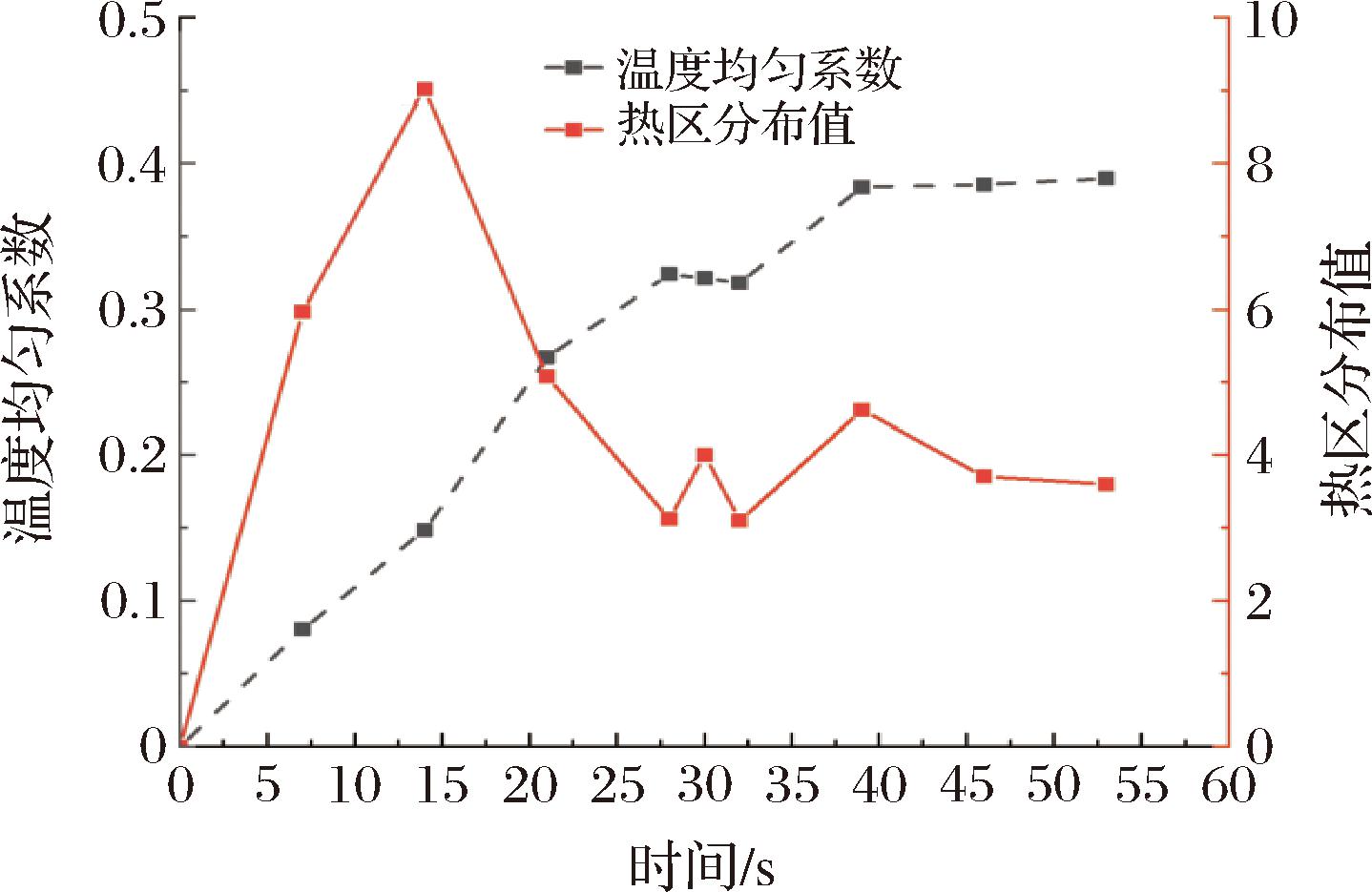
图9 不同加热时间下微波加热样品的温度均匀系数与热区分布值
Fig.9 Temperature uniformity coefficient and hot zone distribution value of microwave heated samples under different heating time
2.3 电磁场拟合结果与分析
2.3.1 翻转前后微波腔体电场分布云图
微波在炉腔内遇到理想电导体会发生全反射,从而形成驻波[18],微波的辐射频率为2.45 GHz,其波长为122.4 mm,驻波为61.2 mm。炉腔长350 mm,除以驻波波长约为6,在X轴方向上形成6个电场强峰。
根据图10可以看出,翻转前与翻转后电场分布情况大致相同,电场强点和弱点的位置基本一致,区别在于场强的最大值和最小值存在明显差异。说明旋转加翻转操作会对谐振腔内电场强度产生削弱作用,但不会改变电场强弱点的分布。
图10 不同加热时间下微波加热模型的电场分布图
Fig.10 Electric field distribution plot of microwave heating model at different times
腔体内电场模分布与均匀系数如图11所示。翻转后各平面均匀系数低于翻转前,翻转中的均匀系数最小,说明增加翻转操作对改善腔体内电场分布的均匀性有一定的促进作用。从电场强度来看,XZ方向上场强高于其他方向,在垂直方向上(Z轴)翻转前后平均场强减小,说明增加翻转操作会对电场有一定的削减作用,可以有效避免腔体内电场强峰的出现。
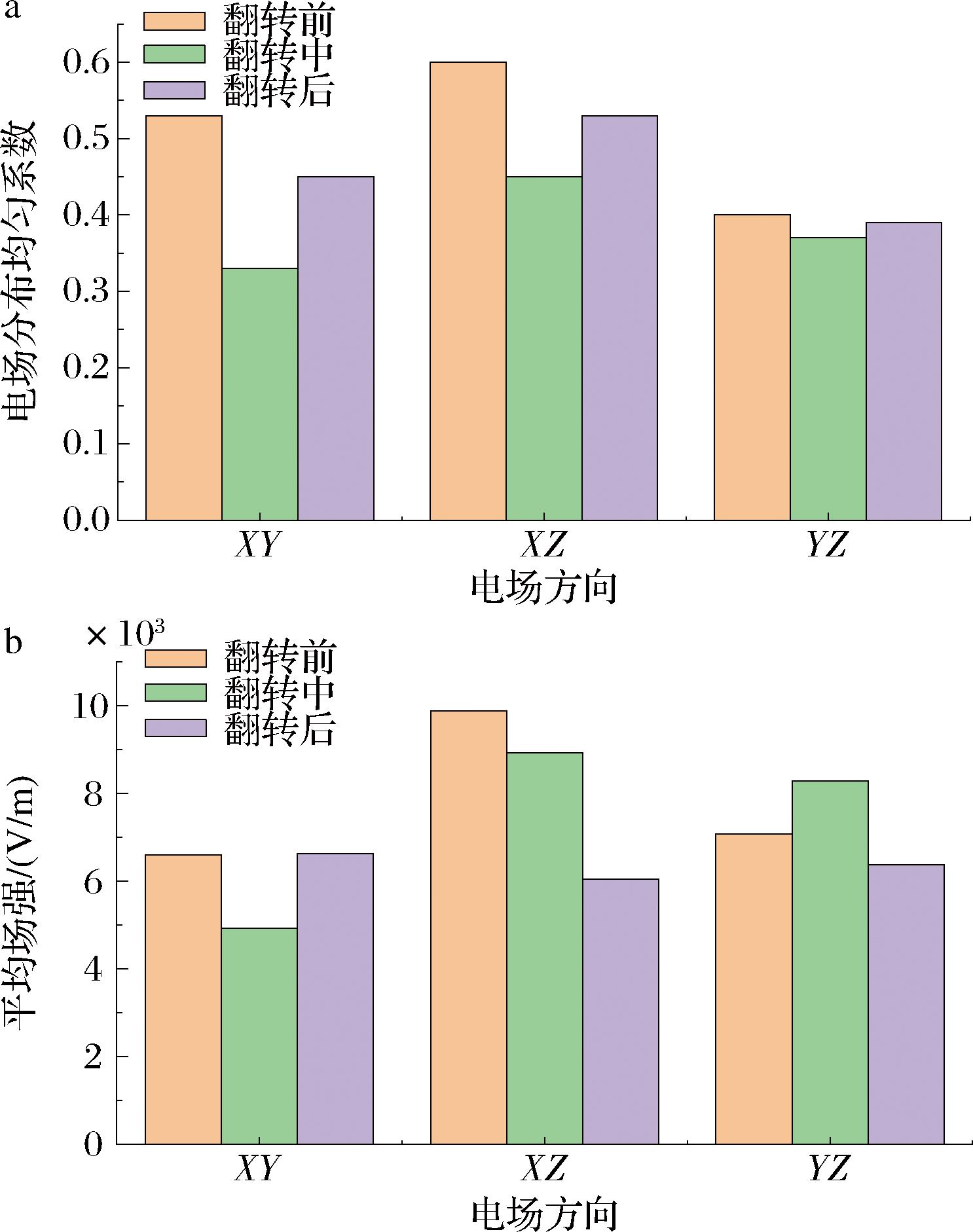
a-腔体电场均匀性;b-腔体电场强度
图11 不同加热时间下加热腔体内的电场强度与均匀系数
Fig.11 Electric field intensity and uniformity coefficient inside the heating chamber under different heating times
2.3.2 翻转前后样品电场分布
鸡腿电场分布与平均电场强度均匀系数变化规律如图12、图13所示。在结构尺寸等固定的微波腔体内,平面波在卤鸡腿上表面射入和射出位置及距离,决定鸡腿内部的电场强度。根据Ei=E0cosθ,其中微波入射角θ值越大,鸡腿电场值越小[19]。所以鸡腿旋转过程中,加热14 s时,鸡腿入射角大于加热7 s时,场强减小呈下降趋势。随着加热进行,θ值变小,场强增加呈上升趋势,导致鸡腿在旋转中出现电场强度先减小再增大的周期变化。微波中电磁波经多次反射会在样品与金属壁间形成复杂电场分布,会导致鸡腿下部份吸收过多微波能[19],同时微波的穿透深度小于鸡腿厚度,能量无法穿透到内部,随着加热时间延长,鸡腿内外场强差异过大,均匀性下降。翻转时,鸡腿周围受纵横电场影响,平均电场强度高于翻转前,均匀系数下降。翻转后,鸡腿平均电场强度高于翻转前,且均匀性较好。可能鸡腿垂直方向上下调换,促进上下层能量利用,避免了鸡腿下部分长时间吸收电场而造成过热,所以翻转后均匀性优于翻转前。
a-7s;b-14s;c-21s;d-28s;e-39s;f-46s;g-53s
图12 不同加热时间时鸡腿的电场分布
Fig.12 Electric field distribution of chicken legs under different heating times
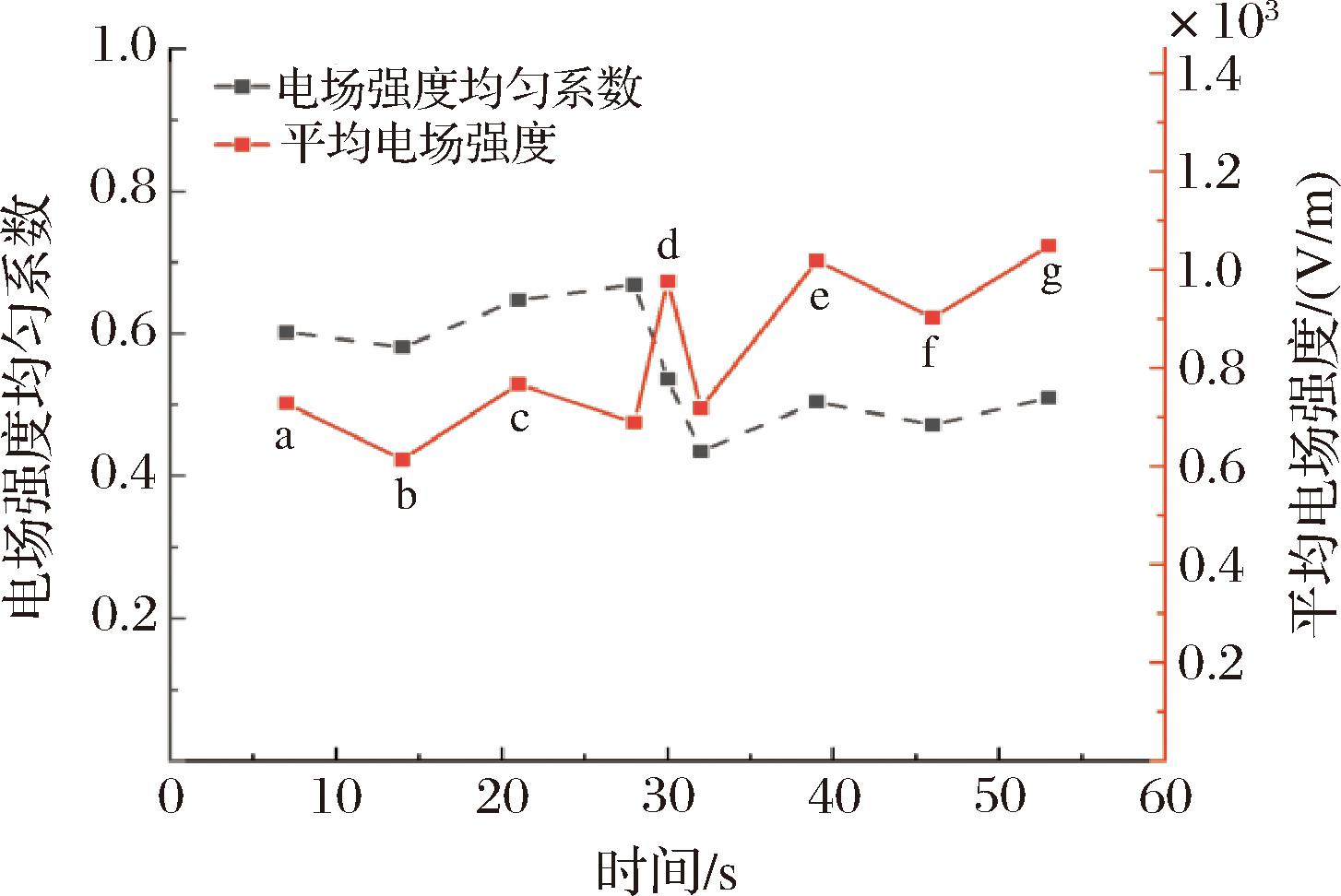
图13 不同加热时间时鸡腿的平均电场强度和均匀系数
Fig.13 Average electric field strength and uniformity coefficient of chicken legs under different heating times
注:a-7s;b-14s;c-21s;d-28s;e-39s;f-46s;g-53s。
鸡腿上下层电场差与均匀系数差如图14所示。由于卤鸡腿上表面入射点和射出点的间距增大,导致翻转前鸡腿上下层场强差逐渐增大,但由于上下层电场较低,所以均匀系数之差出现短暂减小的趋势。随着加热时间延长,鸡腿上下层电场差逐渐增大,不均匀程度也逐渐增大。翻转后,加热时间延长,上下电场强度差与均匀系数差逐渐减小。综上所述,翻转操作可以改善垂直方向上样品的电场差,从而改善微波加热的均匀性。
a-样品上下层电场差与均匀性;b-样品上下层电场分布对比
图14 不同加热时间内鸡腿上下层电场分布与电场强度差和均匀系数差
Fig.14 Electric field distribution, difference in electric field strength, and uniformity coefficient between the upper and lower layers of chicken legs under different heating times
2.3.3 样品电场吸收与电磁损耗均匀系数
单位时间样品的微波能吸收规律与上下层吸收变化如图15与图16所示,对比鸡腿的电场可以发现,微波能吸收趋势等同于其电场强度分布。因为微波能吸收可代表单位功率条件下产生电场强度的大小,与电场强度有一致的变化趋势[20]。微波能吸收随着加热时间的增大而增大,相比翻转前,翻转后上下层体微波能吸收差逐渐降低,均匀系数减小。
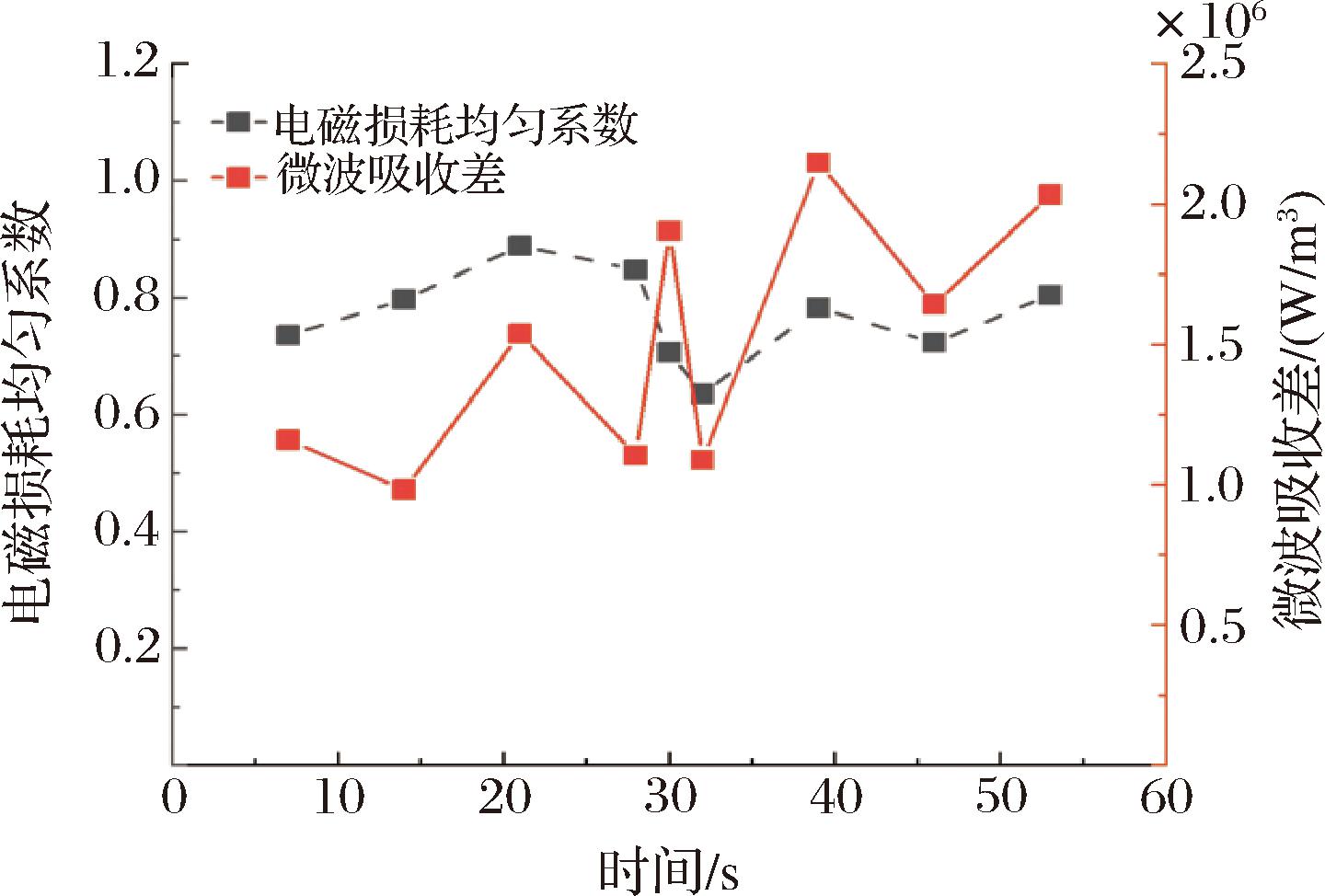
图15 不同加热时间内鸡腿电场分布与平均微波能吸收和均匀系数
Fig.15 Distribution of electric field and average body microwave energy absorption and uniformity coefficient of chicken legs under different heating times
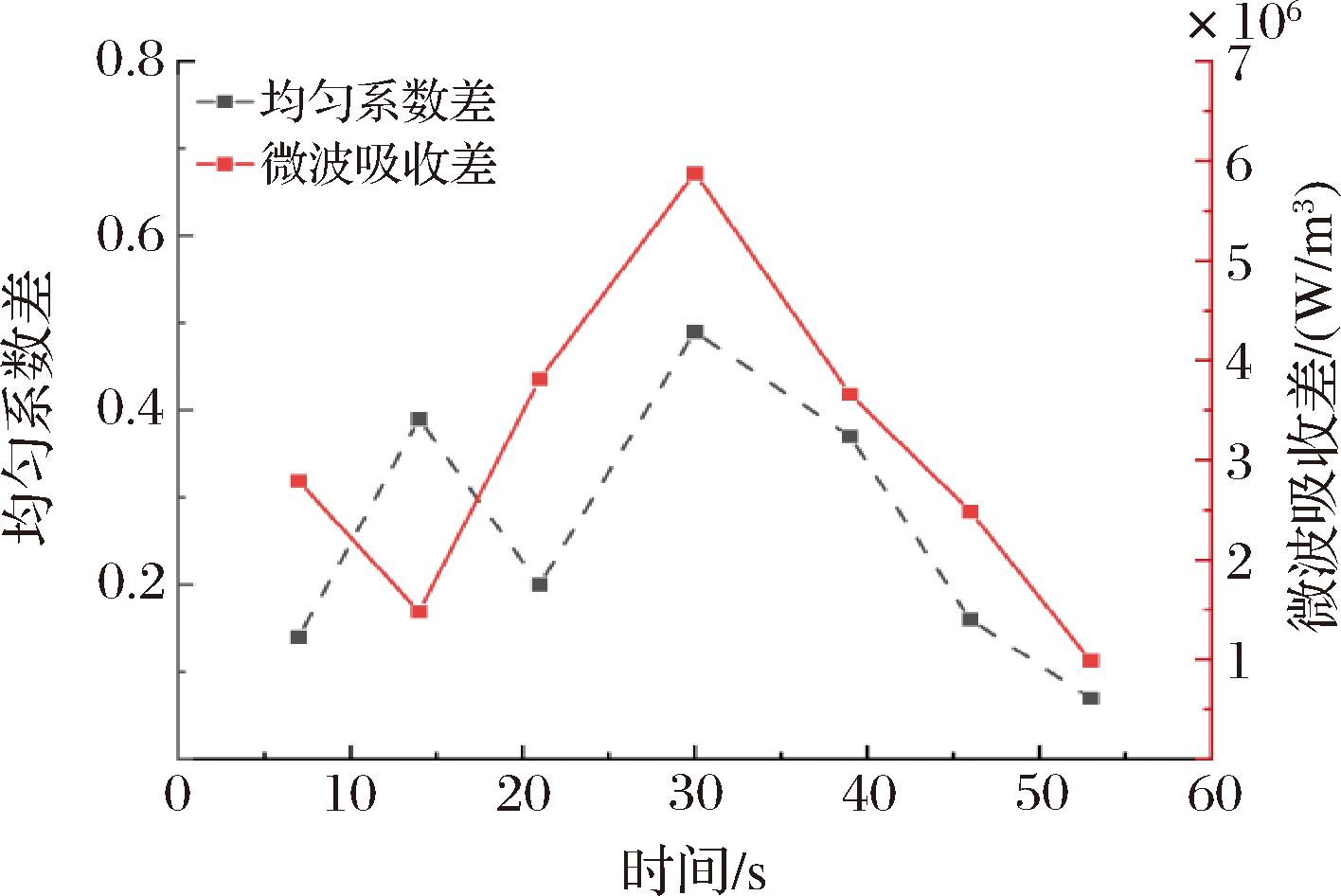
图16 不同加热时间内鸡腿上下层微波能吸收差与均匀系数差
Fig.16 Difference in microwave energy absorption and uniformity coefficient between the upper and lower layers of chicken legs under different heating times
由于微波在右侧波导口输出,从玻璃容器入射到卤鸡腿边缘,形成边缘处电场强度高向内衰减,形成电场强弱分布。随着加热时间延长,造成卤鸡腿在翻转前上下层电场差逐渐增大,微波能吸收均匀系数也增大,不均匀程度明显。卤鸡腿翻转后,上下层鸡腿的微波吸收之差和均匀系数之差逐渐减小,使样品均匀性提高,均匀系数小于翻转前。翻转后鸡腿平均体微波能吸收量高于翻转前,说明翻转操作可以促进微波能的利用效率。综上可得,增加翻转操作可以促进鸡腿上下层微波能的能量吸收,改善微波加热均匀性。
3 结论
本文利用 COMSOL 软件模拟了旋转叠加翻转的微波加热过程,构建了多物理场仿真模型,并验证了模型的可靠性,得出如下结论:
a)微波加热特征点温度模拟值和实验值的RMSE为4.97%,表明本研究建立的多物理场仿真模型能较好地模拟微波加热过程。
b)微波加热中,随着加热时间变化,均匀系数逐渐增大;翻转操作会影响卤鸡肉表面的加热效果,可以有效减少食品在加热中的热区集中,从而改善温度分布不均匀的问题。
c)翻转操作不会明显改变腔内电场分布,可通过减小卤鸡腿上下层的电场差提高卤鸡腿的电场均匀性,均匀的电场分布减小了电场叠加造成的能量损失,提高整体能量效率和温度均匀性。
[1] 张鹏, 颜碧, 李江阔, 等. 果蔬微波联合干燥技术研究进展[J]. 包装工程, 2019, 40(19): 16-23.ZHANG P, YAN B, LI J K, et al. Research progress on microwave combined drying technology of fruits and vegetables[J]. Packaging Engineering, 2019, 40(19): 16-23.
[2] 周明长,李少甫.基于数值仿真的多馈微波加热温度控制系统[J]. 微波学报, 2019, 35(5): 92-96.ZHOU M C, LI S F. Multi-feed microwave heating temperature control system based on numerical simulation[J]. Journal of Microwaves, 2019, 35 (5): 92-96.
[3] 秦庆雨, 郑先哲, 王磊, 等. 树莓果浆微波泡沫干燥过程能量吸收与利用[J]. 食品科学, 2020, 41(15): 124-133. QIN Q Y, ZHENG X Z, WANG L, et al. Energy absorption and utilization during microwave foam drying of raspberry pulp[J]. Food Science, 2020, 41(15): 124-133.
[4] 张柔佳, 王易芬, 栾东磊. 微波加工过程中食品温度分布规律及其均匀性研究[J]. 食品与发酵工业, 2018, 44(4):270-278.ZHANG R J, WANG Y F, LUAN D L. A review of temperature distribution and heating uniformity of food during microwave thermal processing[J].Food and Fermentation Industries, 2018, 44 (4): 270-278.
[5] 易正凯, 谷文静, 许海侠, 等. 数学模拟技术在食品微波加工过程中的应用研究进展[J]. 食品工业科技, 2018, 39(24): 350-356.YI Z K, GU W J, XU H X, et al. Application research progress of numerical simulation technology in food microwave processing[J]. Science and Technology of Food Industry, 2018, 39 (24): 350-356.
[6] 
T K, MIRAN W. Experimental investigation of the combined translational and rotational movement on an inclined conveyor on radio frequency heating uniformity[J]. Innovative Food Science &Emerging Technologies, 2018, 47: 16-23.
[7] YE J H, XIA Y, YI Q Y, et al. Multiphysics modeling of microwave heating of solid samples in rotary lifting motion in a rectangular multi-mode cavity[J]. Innovative Food Science &Emerging Technologies, 2021, 73:102767.
[8] 胡蕾琪, 郭长凯, 栾东磊. 软包装三文鱼片的微波杀菌工艺[J]. 食品与发酵工业, 2020, 46(9):185-189.HU L Q, GUO C K, LUAN D L. Development of microwave pasteurization process for soft-packed Atlantic salmon (Salmo salar) fillet[J]. Food and Fermentation Industries, 2020, 46(9): 185-189.
[9] MENG Q, LAN J Q, HONG T, et al. Effect of the rotating metal patch on microwave heating uniformity[J]. Journal of Microwave Power and Electromagnetic Energy, 2018, 52(2): 94-108.
[10] YE J H, LAN J Q, XIA Y, et al. An approach for simulating the microwave heating process with a slow-rotating sample and a fast-rotating mode stirrer[J]. International Journal of Heat and Mass Transfer, 2019, 140: 440-452.
[11] CHEN J J, PITCHAI K, BIRLA S, et al. Heat and mass transport during microwave heating of mashed potato in domestic oven:Model development, validation, and sensitivity analysis[J]. Journal of Food Science, 2014, 79(10): E1991-E2004.
[12] 卫灵君, 宋春芳, 孟丽媛, 等. 微波加热鸡肉和土豆的传热仿真分析研究[J]. 现代食品科技, 2016, 32(12): 171-177．WEI L J, SONG C F, MENG L Y, et al. Analysis of a heat transfer model for microwave heating of chicken and potato[J]. Modern Food Science &Technology, 2016, 32(12): 171-177.
[13] 曾惠, 滕宇萍, 洪涛, 等. 基于多物理场计算的微波加热能量转换分析[J]. 真空电子技术, 2020(1): 79-82.ZENG H, TENG Y P, HONG T, et al. Energy conversion analysis of microwave heating based on multi-physics field computation[J].Vacuum Electronics, 2020 (1): 79-82.
[14] MIRABITO C, NARAYANAN A, PÉREZ D, et al. FEMLAB model of a coupled electromagnetic-thermal boundary value problem[J]. Research Experience: Worcester Polytechnic Institute, MA, 2005.
[15] 王磊, 沈柳杨, 刘成海, 等. 微波干燥浆果过程中料层电场分布影响能量利用分析[J]. 农业工程学报, 2021, 37(4): 1-10.WANG L, SHEN L Y, LIU C H, et al. Effect of electric field distribution on energy use efficiency for berry puree under microwave drying[J]. Transactions of the Chinese Society of Agricultural Engineering, 2021, 37(4): 1-10.
[16] 张柯, 卢立新, 王军. 基于COMSOL的包装食品微波炉加热模拟[J]. 包装工程, 2014, 35(5):1-4; 12.ZHANG K, LU L X, WANG J. Simulation of microwave heating of packaged food by software COMSOL[J]. Packaging Engineering, 2014, 35 (5): 1-4;12.
[17] 高明. 蓝莓果浆微波干燥均匀性研究[D]. 哈尔滨: 东北农业大学, 2022.GAO M. Study on the uniformity of microwave drying of blueberry pulp[D]. Harbin: Northeast Agricultural University, 2022.
[18] 戴辉明, 郭雯, 程裕东, 等. 不同形状包装食品在微波加热过程中的三维温度分布[J]. 食品工业科技, 2015, 36(13): 82-86;102．DAI H M, GUO W, CHENG Y D, et al. Three dimensional temperature distribution of the packaged foods with different shapes during microwave heating [J]. Science and Technology of Food Industry, 2015, 36(13): 82-86; 102.
[19] LIU S X, FUKUOKA M , SAKAI N. A finite element model for simulating temperature distributions in rotating food during microwave heating[J]. Journal of Food Engineering, 2013, 115(1):49-62.
[20] SADIKU O. Elements of Electromagnetics[M]. New York: Oxford fourth ed, 2007.