预测均方根误差(root mean square error of prediction，RMSEP)、预测集决定系数
范围误差比(ratio of performance to standard deviate, RPD)作为模型的评价指标[21]。当的RMSEC和RMSEP较低(接近于0)且相近，
较高(接近于1)以及RPD值大于3，证明校正模型的预测能力最好、稳定性最强。以上数据分析均在Unscrambler X 10.3(挪威CAMO 公司)中进行。果味啤是一种混合啤酒饮料，因为兼具啤酒的营养物质，较低的苦味和酒精度以及果汁的甜香，近几年逐渐流行起来，深受广大青少年以及女性消费者的喜爱[1-3]。添加果汁来进行菠萝啤的发酵，既能完整地保留果汁的香味又使得风味物质比例均衡，使菠萝啤具有更加独特的口味[4-6]。近几年，一些黑心生产厂家为了追求高额利润采用人工合成香精代替原果汁，导致营养价值极大降低，因此需要重视对其果汁含量的测定。目前我国对于果味啤中的果汁含量的测定还没有相应的国家标准[7]，一般采用推算法测定其果汁含量，虽然这种方法检测结果较准确，但存在检测时间长、方法复杂，同时化学试剂消耗多、对环境污染严重的缺点。因此不适用于快速验证大批量样品中的果汁含量是否符合标识[8-9]。因此研究果味啤中果汁含量的快速检验方法具有深远意义。
近红外光谱(near-infrared spectroscopy, NIR)分析技术作为一种无损检测方法，具有操作简单、分析效率高等优点，由于和化学计量学结合得以广泛使用，目前已经被应用于食品、药品和酿造等行业中[10-17]。张严等[18]研究了近红外结合化学计量学方法在油脂快速检测中的应用，并分析比较了模型的预测效果。樊双喜等[19]采用近红外光谱技术对黄酒进行了无损测定，利用偏最小二乘法分别建立黄酒中的酒精度、总糖等含量的校正模型，模型的准确性较高。然而，目前尚未有采用近红外光谱分析技术对果啤中的果汁含量快速检测的研究。而且大部分的研究采用的均是在全光谱范围内建立偏最小二乘模型，但是由于全光谱中难免包含过多的噪声和无用信息，会对建模的精确度和稳定性造成较大的影响，因此对于有效波长的提取在建模过程中显得尤其重要[14]。
本文以菠萝啤为研究对象，采用NIR分析技术对菠萝啤进行快速检测，并采用特征波长选择方法来提高模型性能，同时探讨向后间隔偏最小二乘(backward interval partial least squares, Bi-PLS)、组合间隔偏最小二乘(synergy interval partial least squares, Si-PLS)、遗传算法(genetic algorithm, GA)优化的偏最小二乘(partial least squares, PLS)回归模型对其果汁含量的预测效果，从而为检测菠萝啤中果汁含量提供一种新方法。
从超市采购的某品牌5个不同批次的菠萝啤(乙醇体积分数0.6%～2.5%、果汁含量0.8%～3.2%)。
NIRMaster傅立叶变换(FT)近红外光谱仪，Buchi(中国)有限公司；光谱光源为卤钨灯，检测器为温控InGaAs。光谱为4 000～10 000 cm-1，分辨率为8 cm-1。
依据GB/T 16771—1997测定果汁含量。
以透射方式采集菠萝啤样品在近红外光谱区域4 000～10 000 cm-1的光谱信息，共计1 501个波长点。
本实验从全部样品中随机选择出35个样品作为独立测试集，用来检测最终建立的模型效果。采用Kennard-Stone (K-S)方法将剩余的110个菠萝啤样品的光谱进行主成分分析(PCA)之后，选用主成分得分为特征变量选择样品[20]按照2∶1的比例对剩下的110个样品进行校正集和验证集的划分，其中校正集包含76个样品，验证集包含34个样品。
对采集的光谱数据进行预处理以后建立PLS模型，以交叉验证的均方根误差(RMSECV)为目标确定最佳的预处理方法，采用的预处理方法包括一阶导数、二阶导数、标准归一化(SNV)、多元散射校正(MSC)。
采用全光谱建模难免会包含一些与待测组分无关的光谱波段，会增加模型计算的复杂度和光谱噪音，波长选择一方面可以简化模型，同时能剔除掉不相关的光谱变量，从而达到增加校正模型预测能力和稳定性的目的，拟采用向后间隔偏最小二乘、组合间隔偏最小二乘、遗传算法3种波长选择算法。
采用Bi-PLS、Si-PLS、GA三种算法提取菠萝啤的特征波长，并结合偏最小二乘(PLS)回归算法建立菠萝啤中果汁含量的校正模型，以校正均方根误差(root mean square error of calibration，RMSEC)、校正集决定系数预测均方根误差(root mean square error of prediction，RMSEP)、预测集决定系数范围误差比(ratio of performance to standard deviate, RPD)作为模型的评价指标[21]。当的RMSEC和RMSEP较低(接近于0)且相近，较高(接近于1)以及RPD值大于3，证明校正模型的预测能力最好、稳定性最强。以上数据分析均在Unscrambler X 10.3(挪威CAMO 公司)中进行。
110个菠萝啤的光谱如图1所示，从图中可以看出，NIR在4 000、4 458、5 164、6 895 cm-1附近存在较强的吸收，同时5 600和5 915 cm-1附近存在2个较弱的吸收峰。其中4 000、4 458 cm-1附近的吸收峰主要是由C-H键和O-H键的伸缩振动所产生的；5 164、6 895 cm-1处的吸收峰主要是由水分和乙醇中的O-H键伸缩振动的一级倍频吸收产生的，因此这2个吸收峰与待测组分无关。5 600和5 915 cm-1处的吸收峰主要来源于CH3中的一级倍频和糖类中的C-H键的组合频和O-H键的伸缩振动。不同菠萝啤样品的光谱没有明显差异，趋势一致，整个4 000～10 000 cm-1区域内光谱的吸光度之间差异较小，但是又不完全重合，这说明样本整体保持一致，而不同样本之间又存在差异。
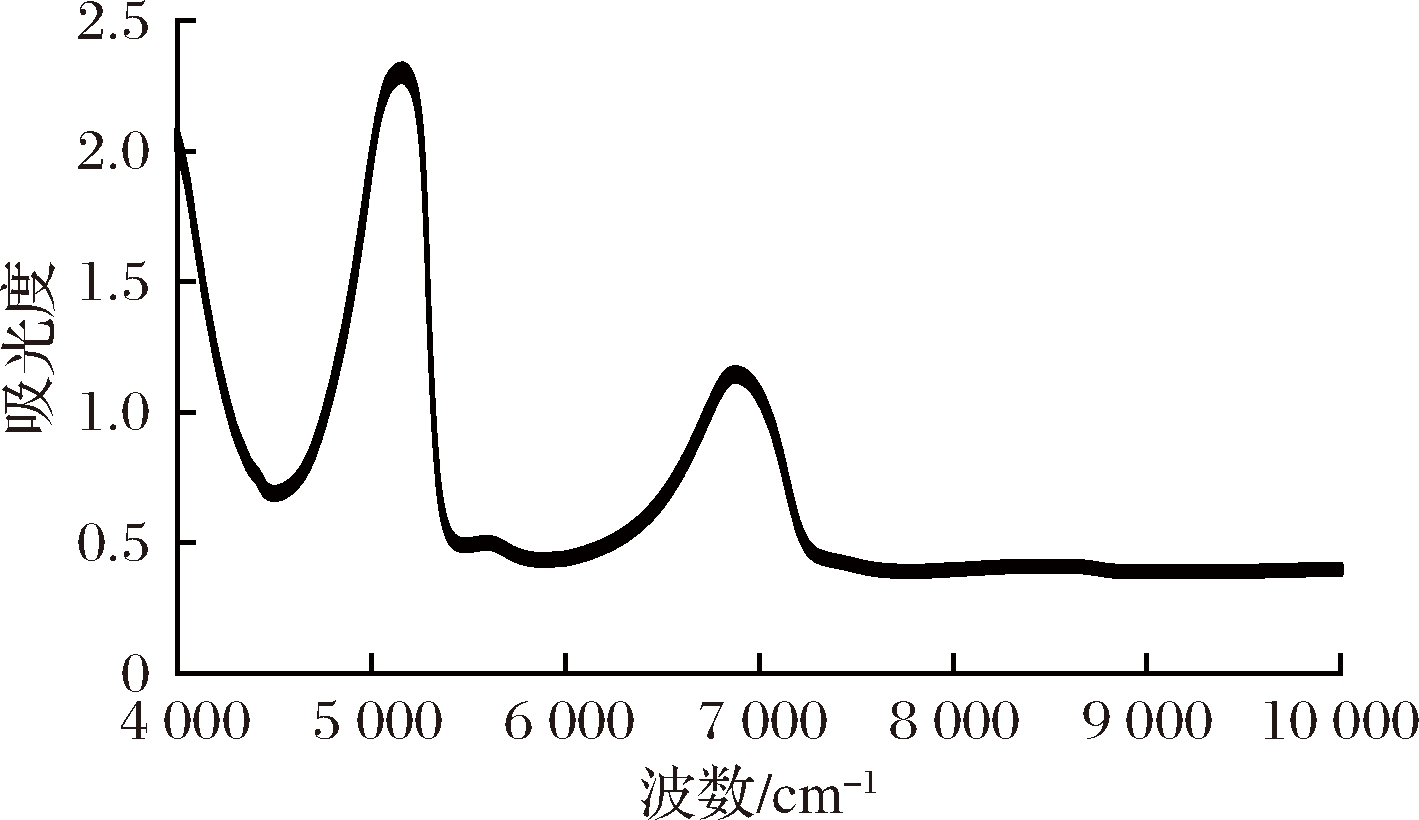
图1 110个菠萝啤的原始近红外光谱
Fig.1 Original near-infrared spectrum of 110 pineapple beer
由于没有异常样品，因此无须剔除样品。样本集的划分结果如表1所示，其中校正集和验证集分布均匀，体现K-S方法选取样品的随机性和代表性。校正集样品完全囊括了验证集，且校正集的偏差与验证集的偏差相差较小，所以符合近红外光谱检测的要求。
表1 校正集与验证集统计结果
Table 1 Calibration set and validation set statistics
样本集样本数最小值/%最大值/%平均值/%标准差/%校正集760.903.162.150.60验证集341.323.072.100.57
图2是经过一阶导数、二阶导数、标准归一化(SNV)、多元散射校正(MSC)这4种预处理方法处理以后的光谱图。
a-一阶导数光谱图；b-二阶导数光谱图；c-SNV光谱图；d-MSC光谱图
图2 各种预处理光谱图
Fig.2 Pretreatment spectra.
将原始光谱进行一阶导数、二阶导数、SNV、MSC这4种预处理以后建立PLS模型，模型的效果如表2所示。
表2 不同预处理方法后建立的PLS模型效果
Table 2 Effect of PLS model established after different
pretreatment methods
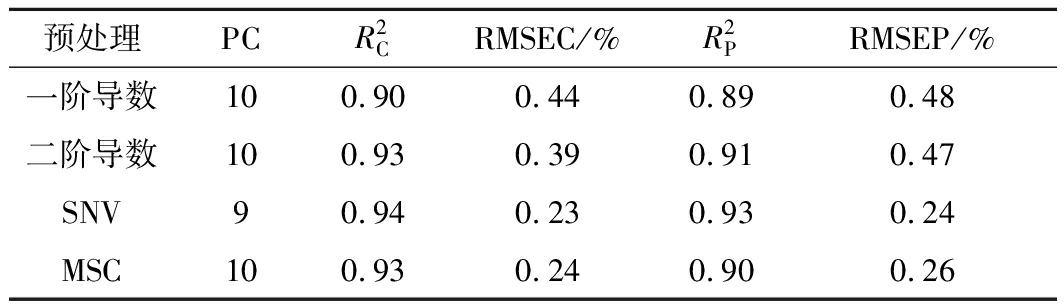
预处理PCR2CRMSEC/%R2PRMSEP/%一阶导数100.900.440.890.48二阶导数100.930.390.910.47SNV90.940.230.930.24MSC100.930.240.900.26
注：PC代表主成分(下同)
由表2可知，光谱经过预处理以后建立的PLS模型对比原始光谱模型的精确度均有所提高，其中采用SNV处理以后模型的性能最优，其中预测集的决定系数
为0.93，RMSEP为0.24%。
2.4.1 Si-PLS的特征波长提取
对原始光谱进行SNV预处理之后所建的PLS模型预测效果要比其他预处理更好，因此最终选择SNV作为预处理方法。Si-PLS是利用不同的频谱区间的组合参与建立PLS回归模型[22-23]。在原始光谱4 000～10 000 cm-1共采集到1 501个光谱波点，因为间隔数量过多过少均会影响到模型效果[24]，所以拟将原始光谱分割为20、25、30、35个区间，分别在组合区间上建模，模型和波长筛选效果如表3所示。
表3 Si-PLS的波段筛选结果
Table 3 Si-PLS band screening results
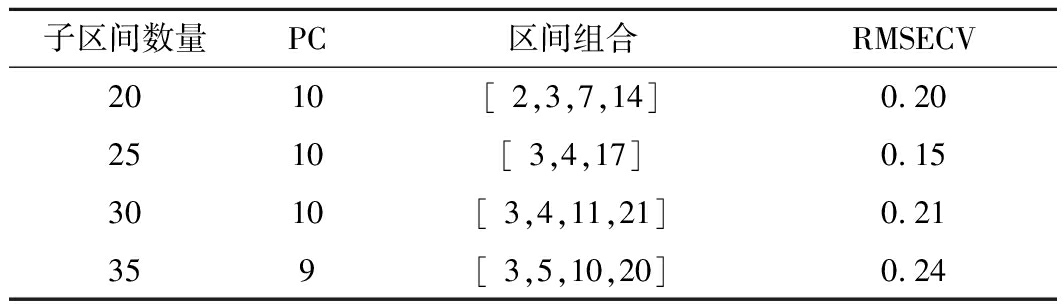
子区间数量PC区间组合RMSECV2010[ 2,3,7,14]0.202510[ 3,4,17]0.153010[ 3,4,11,21]0.21359[ 3,5,10,20]0.24
由表3可知现，当全光谱被分割为25个间隔时，模型的RMSECV为0.15，筛选出的区间组合为[3，4，17]，对应的波段为(4 484～4 960、5 600～6 051、7 844～8 080) cm-1。
2.4.2 Bi-PLS的特征波长提取
和Si-PLS类似[25]，将原始光谱分割为20、25、30、35个间隔，采用Bi-PLS对应不同区间数进行PLS回归，效果如表4所示。
选择最小RMSECV对应的30个区间来分割全光谱，获得的Bi-PLS模型效果最好，RMSECV达到0.19%，优选的最佳的波长区间为[3-5，7，11-13，16，21]，对应的波段为(4 404～5 000, 5 204～5 400, 6 004～6 100, 7 004～7 200, 8 004～8 200) cm-1。
表4 Bi-PLS的波段筛选结果
Table 4 Band screening results for Bi-PLS
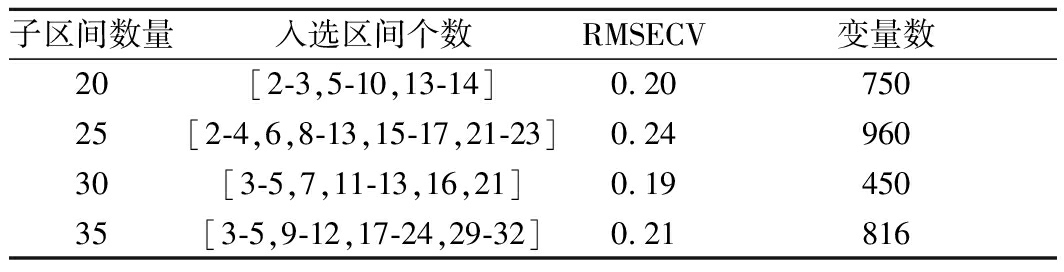
子区间数量入选区间个数RMSECV变量数20[2-3,5-10,13-14]0.2075025[2-4,6,8-13,15-17,21-23]0.2496030[3-5,7,11-13,16,21]0.1945035[3-5,9-12,17-24,29-32]0.21816
2.4.3 GA的特征波长提取
GA的参数设置为初始种群数50，迭代次数为100、交叉率0.6和变异率分别为0.08，传代结束后，频次较多的波点会作为输入变量用来建立PLS模型，以RMSECV值大小确定最优特征波长。由于遗传算法初始群体是随机挑选的，每次筛选的结果都会有差异[26-28, 29-31]，因此为了降低这种情况对结果的影响，进行4次计算，选择模型效果最好的变量作为最优变量。4次计算结果如表5所示，选取83个变量时，RMSECV最小为0.19。图3显示的是第2次计算时各个波点被选用的频率次数，频次最多的区域主要在4 328～9 964 cm-1，其中4 600 cm-1被选用的频次最高。这说明此波段的变量与菠萝啤中果汁信息之间存在较高的相关性。
表5 4次GA计算和选择的变量
Table 5 Four times GA calculation and selected variables
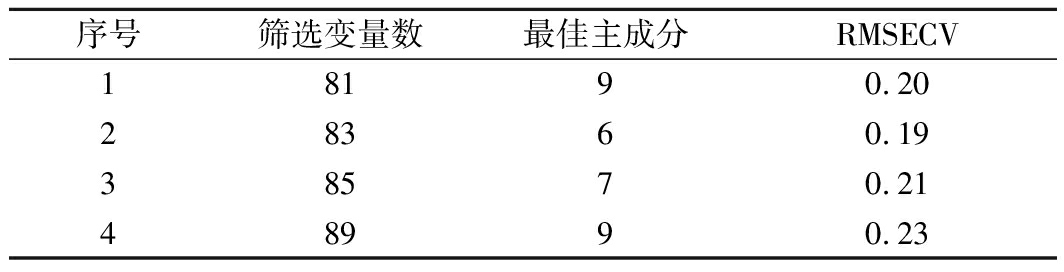
序号筛选变量数最佳主成分RMSECV18190.2028360.1938570.2148990.23
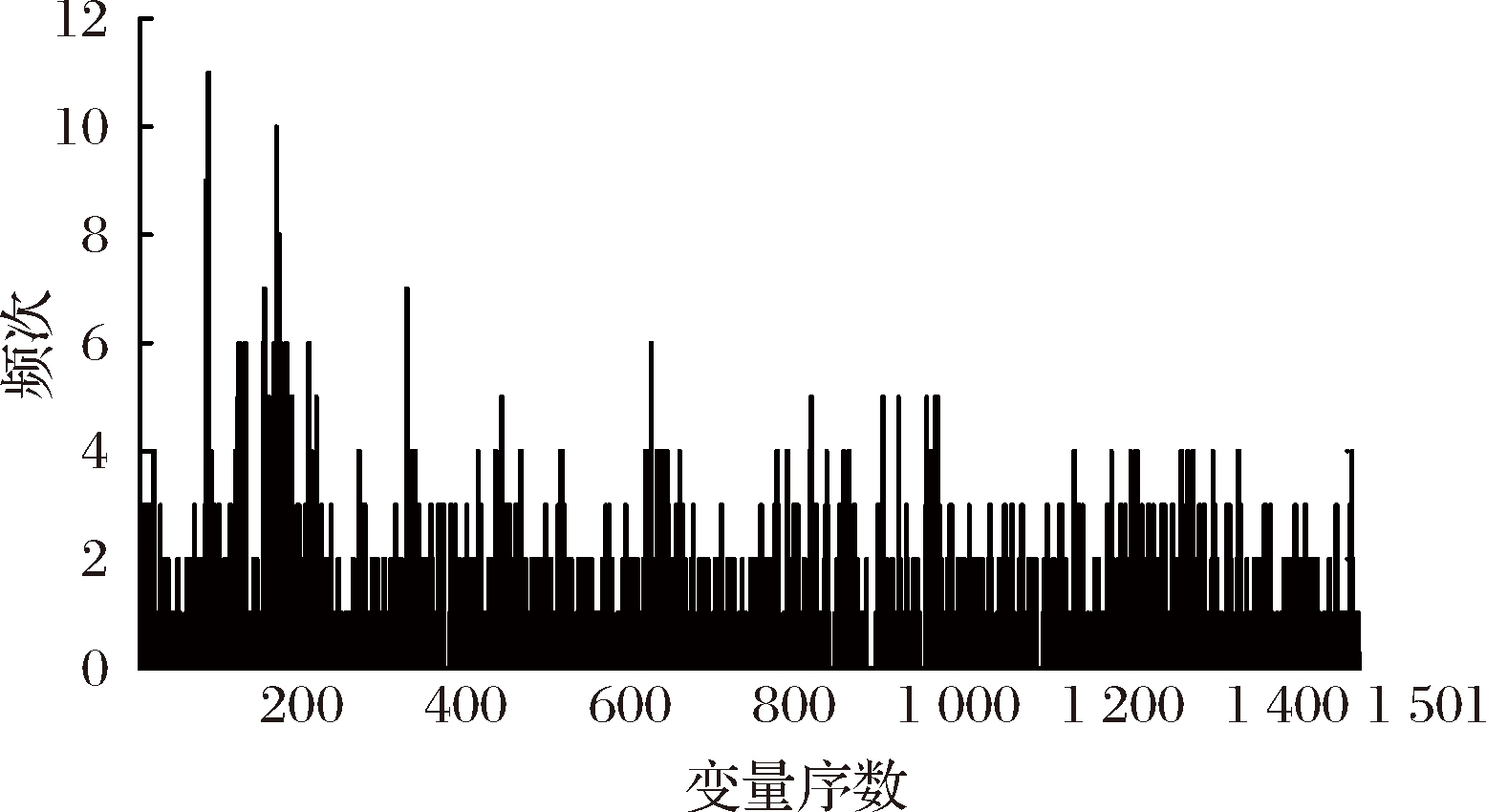
图3 各个波长被选用频次图
Fig.3 Frequency spectrca is selected for each wavelength
图4显示的分别是GA、Si-PLS、Bi-PLS三种方法提取出的特征波长，3种方法筛选得到的特征波段都有重叠的区域，并且6 160、8 080 cm-1左右的波长点均被筛选出来，这说明了这些波长变量都与菠萝啤中果汁含量的特征信息之间存在相关性。
A-GA；B-Si-PLS；C-BiPLS
图4 不同方法挑选的波长变量分布
Fig.4 Wavelength variable distribution selected
by different methods
分析比较了3种提取特征波长的方法，结果如表6所示，用Bi-PLS、Si-PLS、GA算法建立的模型与全光谱模型对比，不仅提高了模型的预测精度，同时极大减少了建模变量。这3种算法提取的特征波长分别为150、94、83，因子数分别为9、9、6。综合比较3种特征波长筛选方法，其中Si-PLS模型的预测集和校正集的精度最高，RMSEC和RMSEP最低，和RPD最高，模型的RMSEP由原始光谱的0.36%减少为0.18%，同时由0.65增大到0.89，RPD由1.63增大到3.17，模型预测精度显著提高，其中提取出的3个特征波段分别为(4 484～4 960、5 600～6 051、7 844～8 080) cm-1，共计94个特征波长。
表6 不同算法特征波长的提取
Table 6 Extraction of characteristic wavelengths of different algorithms
建模方法PC波长/cm-1波点数校正集预测集R2cRMSEC/%R2pRMSEP/%RPD全光谱74 000～10 00015010.880.200.650.361.63Bi-PLS94 404～5 000, 5 204～5 400, 6 004～6 100, 7 004～7 200, 8 004～8 2001500.870.210.840.242.38Si-PLS94 484～4 960, 5 600～6 051, 7 844～8 080940.930.150.890.18 3.17GA64 328～4 352, 4 480～4 516, 4 708～4 896, 5 752, 5 780, 5 876, 6 038～6 492,6 516, 6 548～6 656,7 136～7 488,7 656,7 732,7 922～8 028, 8 600～8 908, 9 124～9 280, 9 404, 9 964830.910.160.880.232.48
GA筛选的波长变量虽然远远少于其他2种算法，但是校正集和预测集的精度低于Si-PLS算法的结果，说明筛选波长能够去除一些无用和多余的信息、极大减少建模的复杂程度，但同时也有可能消除一部分有效的信息使得预测精度降低，所以并不是波长变量越少越好。
图5是Si-PLS提取特征变量在9个因子时的回归系数图，由图5可见，在4 484、4 840、6 044、7 924 cm-1处的回归系数更高，说明这些变量处的光谱信号与菠萝啤果汁含量的线性相关性更好，同时证明Si-PLS筛选出的两个波长区间：4 484～4 960、5 600～6 051、7 844～8 080 cm-1，与Si-PLS筛选的特征波段基本相符。再一次验证了Si-PLS算法提取菠萝啤果汁特征波长的准确性好。
将剩余的35个独立测试集样品导入Si-PLS模型之中，对模型的预测性能进行检验。结果如图6所示，菠萝啤中果汁含量的实测值与预测值线性相关较好，其中R2为0.85，RMSEP为0.19，RPD为3.08，说明Si-PLS模型的预测效果优良。为了进一步验证方法的准确性，通过成对t检验，在置信水平为95%时，P值为0.971 4高于a(0.05)，表明预测值与测量值之间没有显着差异。
图5 Si-PLS筛选波数的回归系数图
Fig.5 Regression coefficient graph of Si-PLS
screening characteristic variables
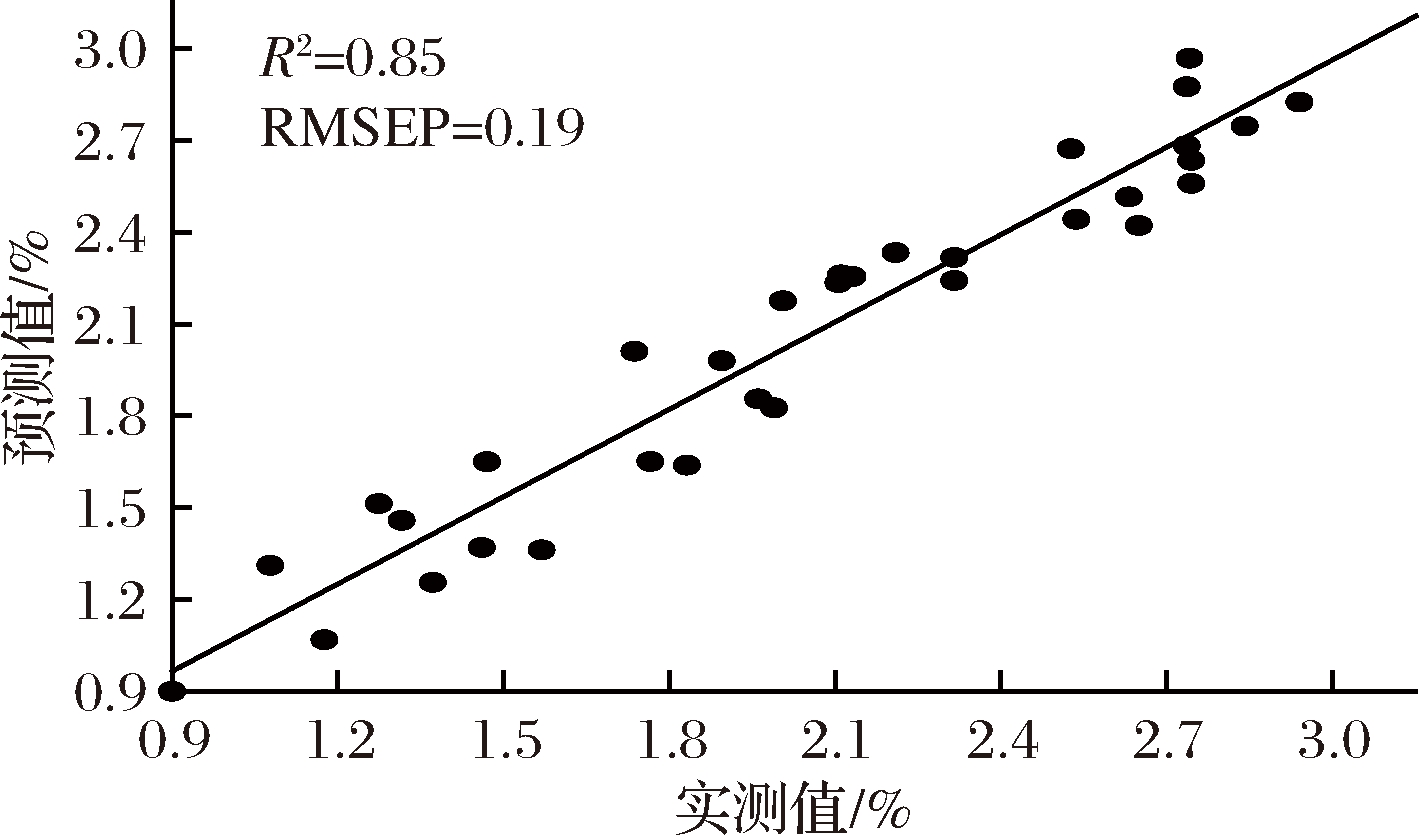
图6 测试集样品的线性回归
Fig.6 Linear regression of test set samples
利用近红外光谱分析技术结合特征波长提取算法建立偏最小二乘(PLS)模型预测菠萝啤中果汁含量。分析比较了3种波长优化算法Bi-PLS、Si-PLS、GA在菠萝啤果汁含量建立的模型效果，研究结果表明，3种方法均能够筛除大量的无关波长变量，其中Si-PLS的效果最好，预测集的RMSEP达到
也达到0.89%，提取出的3个特征波段分别是4 484～4 960、5 600～6 051、7 844～8 080 cm-1，模型得到极大地简化，同时预测能力最好。Bi-PLS、Si-PLS、GA提取的特征变量数分别为150、94、83，其中虽然GA提取的特征变量数最少，但是预测误差要大于Si-PLS，出于模型简化和预测精度两方面的考虑，Si-PLS建立的模型不仅可以减少建模变量，提高建模的分析速度，同时也能提高模型的预测能力，可以作为预测菠萝啤中果汁含量的校正模型。本实验为快速准确测定果啤中果汁含量提供了一种借鉴思路。
[1] 杜冰, 姚汝华. 果汁啤酒的生产与发展趋势[J]. 现代食品科技, 2001, 17(1): 21-22.
[2] 尚静, 张艳. 猕猴桃菠萝啤的研制与品质评价[J]. 农产品加工, 2018, 467(11): 14-16.
[3] 汪中世. 蓝莓菠萝啤研制及其稳定性研究[D]. 合肥：安徽农业大学, 2015.
[4] 宋淑红, 徐慧琴. 6°P菠萝菠萝啤的生产[J]. 农产品加工(学刊), 2014(13): 35-36.
[5] DONG D, LU C, CAO Y, et al. Present situation and development strategy of fruit beer in China[J]. Journal of Food Safety & Quality, 2015，6(7)：2 626-2 632.
[6] 董德武, 卢存龙, 曹圆圆, 等. 我国果汁啤酒生产现状及发展战略[J]. 食品安全质量检测学报, 2015(7):2 626-2 632.
[7] 张亮, 赵长新. 菠萝啤与果汁组分差异的比较[J]. 食品与发酵工业, 2006, 32(9): 149-152.
[8] 谷如祥, 赵武奇, 石珂心,等. 近红外光谱测定苹果饮料中原果汁含量[J]. 食品工业科技, 2013, 34(20): 75-77.
[9] 牛灿杰, 张慧, 王爽,等. 浓缩还原橙汁饮料中果汁含量快速检测方法探究[J]. 食品工业科技, 2015, 36(8): 72- 77.
[10] 褚小立. 近红外光谱分析技术实用手册[M]. 机械工业出版社, 2016.
[11] CHU Xiaoli,LU Wanzhen. Research and application progress of near infrared spectroscopy analytical technology in China in the past five years[J]. Guang Pu Xue Yu Guang Pu Fen XI, 2014, 34(10): 2 595-2 605.
[12] 张世芝, 胡树青, 张明锦. 基于回归系数的变量筛选方法用于近红外光谱分析[J]. 计算机与应用化学, 2012, 29(2): 227-230.
[13] NADLER B, COIFMAN R R. The prediction error in CLS and PLS: The importance of feature selection prior to multivariate calibration [J]. Journal of Chemometrics, 2010, 19(2): 107- 118.
[14] RADY A, GUYER D. Utilization of visible/near-infrared spectroscopic and wavelength selection methods in sugar prediction and potatoes classification[J]. Journal of Food Measurement & Characterization, 2015, 9(1): 20- 34.
[15] MOHAMMADREZA K, MOBEDI H, MOBEDI E, et al. Quantitative determination of naltrexone by attenuated total reflectance - FTIR spectrometry using partial least squares (PLS) wavelength selection [J]. Spectroscopy, 2015, 23(2): 113-121.
[16] SPIEGELMAN C H, MCSHANE M J, GOETZ M J, et al. Theoretical justification of wavelength selection in PLS calibration: Development of a new algorithm [J]. Analytical Chemistry, 1998, 70(1): 35- 44.
[17] CHU Xiaoli, XU Yupeng, LU Wanzhen. Research and application progress of chemometrics methods in near infrared spectroscopic analysis[J]. Chinese Journal of Analytical Chemistry, 2008, 36(5): 702-709.
[18] 张严, 谢岩黎, 孙淑敏. 近红外光谱结合化学计量学方法在油脂检测中的应用[J]. 粮食与油脂, 2015, 225(1): 66-68.
[19] 樊双喜, 钟其顶, 李国辉,等. 近红外光谱法快速检测黄酒的酒精度、总糖和总酸[J]. 中国酿造, 2015, 34(2): 135-138.
[20] 张亮, 赵长新. 果啤与果汁组分差异的比较[J]. 食品与发酵工业, 2006, 32(9): 149-152.
[21] 刘桂松. Vis-NIR光谱判别分析的几类模式识别方法研究[D]. 广州：暨南大学, 2015.
[22] QU FANGFANG, REN DONG, HOU JINJIAN, et al. The characteristic spectral selection method based on forward and backward interval partial least squares[J]. Spectroscopy and Spectral Analysis, 2016, 36(2): 593-598.
[23] SHARIATI-RAD M, MASOUMEH H. Selection of individual variables versus intervals of variables in PLSR [J]. Journal of Chemometrics, 2010, 24(2): 45-56.
[24] DENG BAICHUAN, YUN YONGHUAN, MA PAN, et al. A new method for wavelength interval selection that intelligently optimizes the locations, widths and combinations of the intervals [J]. The Analyst, 2015, 140(6): 1 876-1 885.
[25] AHLINDER J, NORDGAARDA. Chemometrics comes to court: Evidence evaluation of chem-bio threat agent attacks[J]. Journal of Chemometrics, 2015, 29(5): 267-276.
[26] 雷英杰, 张善文. MATLAB遗传算法工具箱及应用[M]. 西安：西安电子科技大学出版社, 2014.
[27] MARIANI, NATH
LIA C T, et al. Predicting soluble solid content in intact jaboticaba [Myrciaria jaboticaba (Vell.) O. Berg] fruit using near-infrared spectroscopy and chemometrics [J]. Food Chemistry, 2014, 15(9): 458-462.
[28] 马永杰, 云文霞. 遗传算法研究进展[J]. 计算机应用研究, 2012, 29(4): 1 201-1 206.
[29] LU I R R, KWAN E, THOMAS D R, et al. Two new methods for estimating structural equation models: An illustration and a comparison with two established methods. [J]. International Journal of Research in Marketing, 2011, 28(3): 258-268.
[30] LEARDIR. Application of genetic algorithm-PLS for feature selection in spectral data sets [J]. Journal of Chemometrics, 2010, 14(5-6): 643-655.
[31] HUANG GUANGZAO, RUAN XIUKAI, CHEN XIAOJING, et al. A segmented PLS method based on genetic algorithm [J]. Analytical Methods, 2014, 6(9): 2 900-2 908.